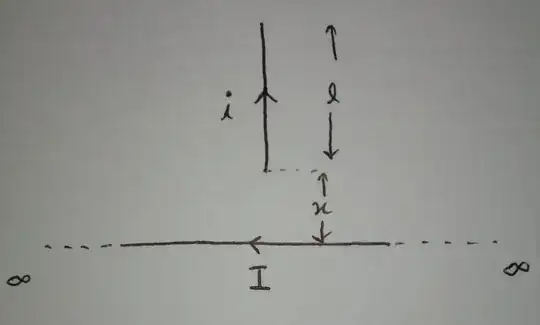
 Question:- Find magnetic force between wires as shown in figure. The infinte wire with current 'I' and the small finite wire of length 'l' with current 'i' at a distance of x from infinte wire (direction shown in figure).
Question:- Find magnetic force between wires as shown in figure. The infinte wire with current 'I' and the small finite wire of length 'l' with current 'i' at a distance of x from infinte wire (direction shown in figure).
I got force on small wire in negative x-axis direction. But as Newton's third law says, for every action there is an equal and opposite reaction. So according to this there must be same magnitude of force applying on infinite wire in positive x-axis (like that in second figure)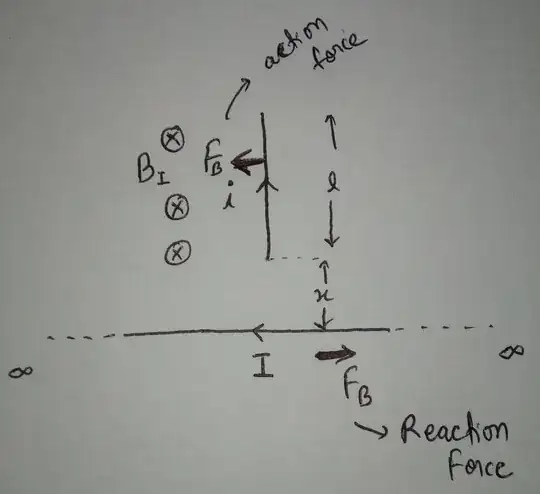 But how is this possible, because of magnetic field of finite wire, we have simple cross product for force so force must be perpendicular to both L and B but here it is parallel to L. (L is length vector and B is magnetic field vector)
Now if we go particularly for small wire we get something like this(in figure 3)
But how is this possible, because of magnetic field of finite wire, we have simple cross product for force so force must be perpendicular to both L and B but here it is parallel to L. (L is length vector and B is magnetic field vector)
Now if we go particularly for small wire we get something like this(in figure 3)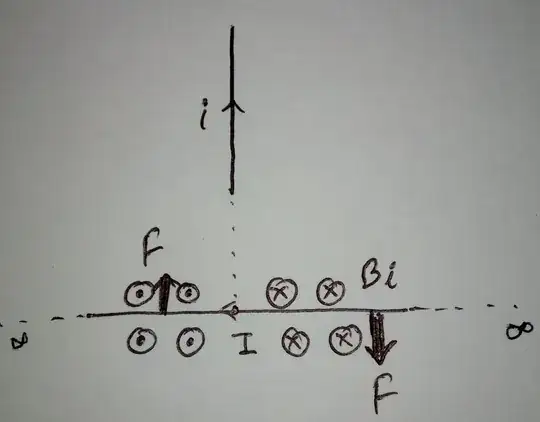 We get torque and F net on infine wire equals to zero. How is this even possible. Neither we are getting force in opposite direction nor of same magnitude. Does this question violates Newton's third law? But this can't. I am sure something I am missing. Please help me through this!
Are there more general cases like this where problem like this arises?
We get torque and F net on infine wire equals to zero. How is this even possible. Neither we are getting force in opposite direction nor of same magnitude. Does this question violates Newton's third law? But this can't. I am sure something I am missing. Please help me through this!
Are there more general cases like this where problem like this arises?
Edit:
I was asked in comments that how I solved for force, so here it is