Does it make sense to model the kinetic energy as:
$$T=\frac{1}{2}mv\,|v| \ \ \ \text{instead} \ \text{of} \ \ \ T=\frac{1}{2}mv^2 \ \ \ ?$$
In the following youtube video, it is explained for an airfoil, why the classic Bernoulli Law description is not enough to explain how much lift is generated in reality. I am not interested in the topic of the video "per se", but in the construction of his explanation. The author uses the Bernoulli Equation to group the terms associated with the kinetic energy of the fluid. After some manipulation, using it to built the Drag Force proportional to a quadratic term of the velocity, giving intuition of why it is modeled as:
$$F_d=\frac{1}{2}\rho A\,C_d\,v^2$$
Now, I would like to review a simple and well known example of a physics model, where the drag force is considered, the classic nonlinear pendulum with friction.
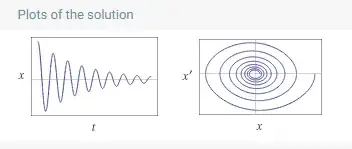
If the classic nonlinear pendulum with the friction equation is reviewed, where the drag force is modeled proportional to the speed, as in Stokes' Law, in Wolfram-Alpha. It can be seen that it has decaying solutions as expected:
$$\ddot{x}+2\cdot0.021\,\dot{x}+0.2\sin(x)=0, \ \ \ \\ x(0)=\frac{\pi}{2}, \ \ \ \ \dot{x}(0)=0 \tag{Eq. 1}\label{Eq. 1}$$
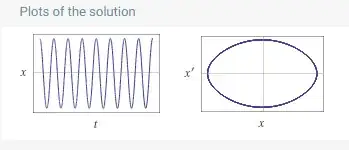
If instead, the standard drag force $F_{\text{drag}}\propto (\dot{x})^2$ is used as is shown here for the equation:
$$\ddot{x}+0.021(\dot{x})^2+0.2\sin(x)=0, \ \ \ \ \\ x(0)=\frac{\pi}{2}, \ \ \ \ \ \dot{x}(0)=0 \tag{Eq. 2}\label{Eq. 2}$$
their solution isn't showing the expected decay one can see on the experimental pendulums.
This issue could be solved using an ansatz for the drag force $F_{\text{drag}}\propto \dot{x}|\dot{x}|$ (following this reference equation $1.127$), which as can be seen here for the equation:
$$\ddot{x}+0.021\dot{x}|\dot{x}|+0.2\sin(x)=0, \ \ \ \ \\ x(0)=\frac{\pi}{2}, \ \ \ \ \ \dot{x}(0)=0 \tag{Eq. 3}\label{Eq. 3}$$
their solution has recovered again the expected decaying behavior for a pendulum with friction.
Now, given the close relation between the kinetic energy and the drag force shown on the video, and due the failing of the classic form of the drag force to reproduce the decaying solutions of a pendulum with friction, I would like to know if make sense to consider the kinetic energy as:
$$T=\frac{1}{2}mv\,|v| \ \ \ \text{instead} \ \text{of} \ \ \ T=\frac{1}{2}mv^2$$
I hope you could explain why that is so, and if there are any examples, sharing them and explaining how the kinetic energy term $T\propto v\,|v|$ has arisen. For a negative answer, please elaborate, explaining why the standard equation of the drag force shown in Wikipedia fails at describing the pendulum with friction as shown in \eqref{Eq. 2} but it works for \eqref{Eq. 3} (in this paper at point $III$ is even solved piecewise).
Added Later
These are the calculation done in the mentioned youtube video:
$$\begin{array}{l} \text{velocities on upper/lower sides of the airfoil}\quad v_1=\frac{d_1}{t_1}; \quad v_2=\frac{d_2}{t_2}; \\ \text{assumption}\quad t_1=t_2\ \ \textit{(mistaken)}\\ \text{Bernoulli Equation} \qquad P_1 + \rho g h + \underbrace{\frac{1}{2}\rho v_1^2}_{\text{kinetic energy}} = P_2 + \rho g h + \underbrace{\frac{1}{2}\rho v_2^2}_{\text{kinetic energy}} \\ \Rightarrow \Delta P = \frac{1}{2}\rho\left(v_2^2-v_1^2\right) = \frac{1}{2}\rho\left(\left(\frac{v_2+v_1}{v_1}\right)\left(\frac{v_2-v_1}{v_1}\right)\right)v_1^2 = \frac{1}{2}\rho\left(\left(\frac{v_2}{v_1}+1\right)\left(\frac{v_2}{v_1}-1\right)\right)v_1^2 \\ \Rightarrow \Delta P = \frac{1}{2}\rho\left(\left(\frac{d_2}{d_1}+1\right)\left(\frac{d_2}{d_1}-1\right)\right)v_1^2 = \frac{1}{2}\rho\left(\left(\frac{d_2}{d_1}\right)^2-1\right)v_1^2 \\ \text{multiplying both sides by area} \Rightarrow \underbrace{A\Delta P}_{F_d} = \frac{1}{2}\rho A \left(\left(\frac{d_2}{d_1}\right)^2-1\right) v_1^2 \underbrace{\propto}_{\text{proportional}} \frac{1}{2}\rho A\,C_d\,v_1^2 \end{array}$$
since from the kinetic energy part of the Bernoulli Equation the video find the Drag Force for the example, I made the pairing with the version were the absolute value is used. Hope this better explain why the question arises.
2nd added later
I found this paper:
where the autors on equations $(59)$ and $(60)$ introduce a Drag Force $F_d = b\ \dot{y} + c\ \dot{y}|\dot{y}|$ for a more accurate description of the air effects on the pendulum. I don't know if it add info about the Kinetic Energy question, but it make sense of the signs required for the proper description of the drag force.