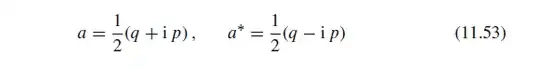The ONLY thing that we know about $p$ and $q$ is their commutation relation $[q,p]=2i$.
In other words, can we find some Hilbert basis such that one of them has the form
I am asking this because it seems to be implied in my introductory QM textbook, although I might be interpreting it wrong and additional assumptions needs to be made about $p$ and $q$.
Well, using your commutation relation
\begin{equation} \begin{split} [\hat{a}, \hat{a}^{\dagger}] &= \frac{1}{4}[q+ip, q-ip] \\ &= -\frac{i}{2}[q, p] \\ &=1 \end{split} \end{equation}
which does indeed produce the canonical commutation relation of ladder operators. However, we can only describe the operators $\hat{a}/\hat{a}^{\dagger}$ as ladder operators if they also satisfy
\begin{equation} \begin{split} [\hat{H}, \hat{a}] = -c\hat{a} \\ [H, \hat{a}^{\dagger}] = c\hat{a}^{\dagger} \end{split} \end{equation}
for some constant $c$ and where the Hamiltonian is $H$. The reasoning for this is that if $|\psi_{n}\rangle$ and $E_{n}$ and an eigenstate and eigenvalue respectively, i.e.
\begin{equation} H|\psi_{n}\rangle = E_{n}|\psi_{n}\rangle \end{equation}
then this implies
\begin{equation} \begin{split} \hat{H}\hat{a}|\psi_{n}\rangle = (E_{n} - c)\hat{a}|\psi_{n}\rangle \\ \hat{H}\hat{a}^{\dagger}|\psi_{n}\rangle = (E_{n} + c)\hat{a}^{\dagger}|\psi_{n}\rangle. \end{split} \end{equation}
While it might be possible to find operators $\hat{a}/\hat{a}^{\dagger}$ satisfying the commutation relations, they may not be particularly useful as raising or lowering operators given the particular form of the Hamiltonian.
Any operator $\hat \Omega$ of the form that you suggest, with entries just above or below the diagonal, can be considered as a raising or lowering operator. Such an operator would have the property that $$ \hat\Omega\vert p\rangle=c_p\vert p\pm 1\rangle $$ and so “ladders down” or “ladders up” depending on how you order basis states.
An example beyond $\hat a$ and $\hat a^\dagger$ would be $\hat L_\pm$, where the ladder operators commute to a diagonal operator; both $\hat L_\pm$ have the same form as suggested by the OP, although the matrix elements are not simple $\sqrt{n}$ form.
In general such ladder operators are quite generic to semi-simple Lie algebras, where root vectors are considered ladder operators, and basis vectors are eigenstates of Cartan elements. Once one defines an ordered set of basis states (often eigenstates of some commuting set of operators), it is of course possible to extend the notion of ladder operators without reference to semi-simple Lie algebras
The answer is in general negative, but it is technical.
If there existed such a Hilbert basis, by construction, the basis would be included in the domains of the Hermitian operators $X$ and $P$.
As a consequence, they would be symmetric as and they would admit selfadjoit extensions given by the standard selfadjoint operators $X$ and $P$ in $L^2(R)$ up to a unitary transformation. This transformation is the one that sends the basis into the standard basis of Hermite functions in $L^2(R)$.
The obstruction is now that it is possible to define operators $X$ and $P$ which satisfies the usual CCR on a common subspace of their domains (and this is equivalent to your CCR for the associated $a$ and $a^\dagger$), but such that there are *no" selfadjoint extensions for $P$.
Tipically, $X$ and $P$ defined on $L^2([0,+\infty))$ as the usual differential operators with common domain given by the space of smooth functions which smoothly vanish at $x=0$.
It is however possible to add some hypotheses to yours to prove your assertion.
In particular, the operator $a^\dagger a$ must be essentially selfadjoint on its domain and there must not exist dense invariant subspaces under the action of $a$ and $a^\dagger$. That is an alternative formulation of the Stone von Neumann theorem.
A more rough set of assumptions which guarantee the validity of your assertion is the following one.
There exists a vector $\psi$ in the domain of $a$ such that $a\psi=0$.
The domain of the two operators includes an invariant subspace which, in turn, contains $\psi$.
The space of finite linear combinations of the vectors $(a^\dagger)^n \psi$ is dense in the Hilbert space.
