How to get the density parameter of $\Lambda$CDM as a function of time?

Question

For flat universe, the Friedmann equation is given by:

$$ H^2 = \frac{8\pi G}{3} ~~ \left( \rho_m + \rho_r + \rho_\Lambda \right). $$

From this thread:

What is the equation for the scale factor of the universe..

we can get the scale factor. As I understand using that:

$ \rho_{m} = \frac{constant}{a^3}= \frac{\rho_{m0}}{a^3} ,~ \rho_{r} = \frac{constant}{a^4} = \frac{\rho_{r0}}{a^4} $

Then:

$ \Omega_{m0} = \frac{8 \pi G}{3H_0^2} ~\rho_{m0}, ~\Omega_{r0} = \frac{8 \pi G}{3H_0^2} ~\rho_{r0},~ \Omega_{\Lambda0} = \frac{8 \pi G}{3H_0^2} ~\rho_{\Lambda0}, $ which gives Friedmann equation by:

$$ H^2 = H^2_0~~ \left( \Omega_{m0} a^{-3}+ \Omega_{r0} a^{-4} + \Omega_{\Lambda0} \right). $$ I’m a little confused how to get the total density parameter $\Omega_{total} = \Omega_{m} + \Omega_{r} + \Omega_{\Lambda} $ as a function of time?

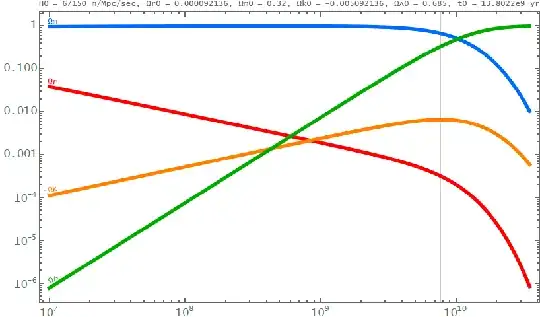
For instance as in this paper arXiv:1709.06497v2 figure (2).

Any help is appreciated!

Answer 1

Dr. phy wrote: "I’m a little confused how to get the total density parameter Ωtotal=Ωm+Ωr+ΩΛ as a function of time?"

First you need the critical density:

$$\rm \rho_c=\frac{3 H^2}{8 \pi G}$$

The Omegas are just the respective densities divided by the critical density:

$$\rm \Omega_{\mu}=\frac{\rho_{\mu}}{\rho_c}$$

with $\rm \mu = r, \ m, \, k, \ \Lambda$ for radiation, matter, curvature & dark energy:

$$\rm \rho_r=\frac{\rho_{r0}}{a^4} \ , \ \ \rho_m=\frac{\rho_{m0}}{a^3} \ , \ \ \rho_k=\frac{\rho_{k0}}{a^2} \ , \ \ \rho_{\Lambda}=\rho_{{\Lambda}0} $$

so you add them all up. In a flat universe:

$$\rm \Omega_{total}=\frac{\rho_r+\rho_m+\rho_{\Lambda}}{\rho_c}=1$$

all the time, while in a curved one:

$$\rm \Omega_{total}=\frac{\rho_r+\rho_m+\rho_k+\rho_{\Lambda}}{\rho_c}\neq1$$

then the volume and curvature radius is:

$$\rm V=2 \pi^2 r_k^3\ , \ \ r_k=\frac{c}{H \sqrt{-\Omega_k}}$$

($2 \pi$ times that and a straight line closes in on itself) with:

$$\rm \Omega_k=1-\Omega_{total}$$

and $\rm H$ as a function of $\rm a$:

$$\rm H(a)=H_0 \sqrt{\Omega_{r0}/a^4+\Omega_{m0}/a^3+\Omega_{k0}/a^2+\Omega_{\Lambda 0}}$$

Since you want it as a function of $\rm t$ the relation to $\rm a$ is:

$${\rm t}=\int_0^{\rm a} \frac{{\rm d}a}{a {\rm H}(a)}$$

For a plot of the density evolution in a flat universe as it is favored by observation see here, and below the same for a hypothetical closed universe (the $\rm x$ axis is $\rm t$ in years):

The first vertical Gridline marks the beginning of the accelerated expansion at $\rm \ddot{a}=0$ which is also where $\rm \Omega_k$ would have its peak, the second one marks the time when $\rm a=1$.