Dr. phy asked: "can we simply get the scale factor $\rm a$ as a function of time?"
For the complete solution containing $\rm \Omega_{r}, \ \Omega_{m}, \ \Omega_{\Lambda}$ simultaneously you have to integrate numerically, but since at all stages of the universe only one or two components dominate while at least one component can be neglected you can use the analytical 1- and/or 2-component solutions for the specific times and glue them together where their values approach each other.
The full solution where you set your neglible components to $0$ and solve for $\rm a $ is
$$\rm \frac{\dot{a}}{a}=H=H_0 \sqrt{\Omega_{r}/a^4+\Omega_{m}/a^3+\Omega_{k}/a^2+\Omega_{\Lambda }}$$
For the purely radiation dominated era right after the big bang you get ↘
$$ \rm a=\sqrt{2 \ H_{0} t} \ \Omega_{r}^{1/4} $$
When matter becomes relevant too we have two solutions, the first is ↘
$$ \rm a=(-i \left(\sqrt{3}-i\right) \sqrt[3]{\sqrt{3} \ \Omega_{m} \left| f-4 \ \Omega_{r}^{3/2}\right| \sqrt{H_{0} \ t \left(f-8 \ \Omega_{r}^{3/2}\right)}+f^2-8 \ f \ \Omega_{r}^{3/2}+8 \ \Omega_{r}^3}$$
$$ \rm +(4 \ i \left(\sqrt{3}+i\right) \Omega_{r}^2)/(\sqrt[3]{\sqrt{3} \ \Omega_{m} \left| f-4 \ \Omega_{r}^{3/2}\right| \sqrt{H_{0} \ t \left(f-8 \ \Omega_{r}^{3/2}\right)}+f^2-8 \ f \ \Omega_{r}^{3/2}+8 \ \Omega_{r}^3})$$
$$ \rm +2 \left(1+i \ \sqrt{3}\right) \Omega_{r}+2 \left(1-i \ \sqrt{3}\right) \Omega_{r})/(4 \ \Omega_{m})$$
The 2nd solution is valid for the 2nd part of the radiation and matter dominated era ↘
$$ \rm a=(\sqrt[3]{\sqrt{3} \ \Omega_{m} \left| f-4 \ \Omega_{r}^{3/2}\right| \sqrt{H_{0} \ t \left(f-8 \ \Omega_{r}^{3/2}\right)}+f^2-8 \ f \ \Omega_{r}^{3/2}+8 \ \Omega_{r}^3}$$
$$ \rm +\frac{4 \ \Omega_{r}^2}{\sqrt[3]{\sqrt{3} \ \Omega_{m} \left| f-4 \ \Omega_{r}^{3/2}\right| \sqrt{H_{0} \ t \left(f-8 \ \Omega_{r}^{3/2}\right)}+f^2-8 \ f \ \Omega_{r}^{3/2}+8 \ \Omega_{r}^3}}+2 \ \Omega_{r})/(2 \ \Omega_{m})$$
When radiation becomes neglible and matter alone dominates we have ↘
$$ \rm a=\left(\frac{3}{2}\right)^{2/3} \ (H_{0} \ t)^{2/3} \ \Omega_{m}^{1/3} $$
When dark energy and matter play together it becomes ↘
$$ \rm a=\sqrt[3]{\frac{1}{\Omega_{\Lambda} }-1} \ \sinh ^{2/3}\left(3 \ H_{0} \ t \ \sqrt{\Omega_{\Lambda} }/{2} \right)$$
The function $\rm f$ which was used for brevity is
$$ \rm f = 3 \ H_{0} \ t \ \Omega_{m}^2$$
Since the radiation dominated era is so short, on a linear plot the last equation for $\rm a$ is good enough if you don't zoom in on the first few million years.
On a logarithmic plot however it makes a difference if you also show the early times. The $\rm x$-axis is $\rm t$ in years, $\rm y$ is the dimensionless scale factor $\rm a$:
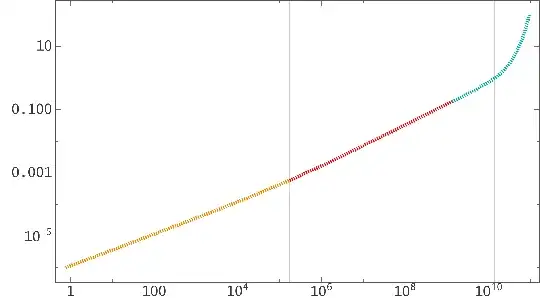
The two component solution is not exact and with my method it deviates about $\rm 0.1 \% $ from the numerical solution (so on a diagram you won't see any difference larger than a pixel on a monitor). Right after the big bang the numerical solution is more exact though, the oscillations in the deviation come from the numerical integration, see the deviation
$$\rm |1-\frac{a_{analytic}}{a_{numeric}}|$$
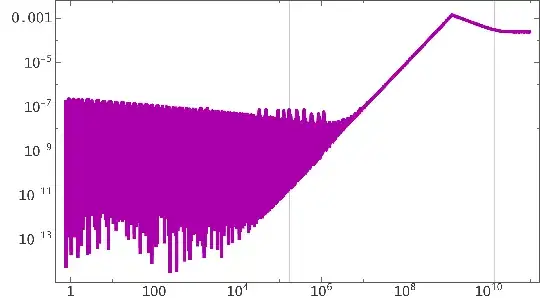
The numerical precision depends on your method and computional ressources, but at some point when $\rm t$ is small enough the analytical solution will be better, since the radiation really dominates at very small $\rm t$.






