10

It is well-known that in TI-symmetric semi-metals the Berry curvature on the Brillouin torus vanishes away from the nodal points (eg. [XCN10, III.B] [Van18, p. 105]).

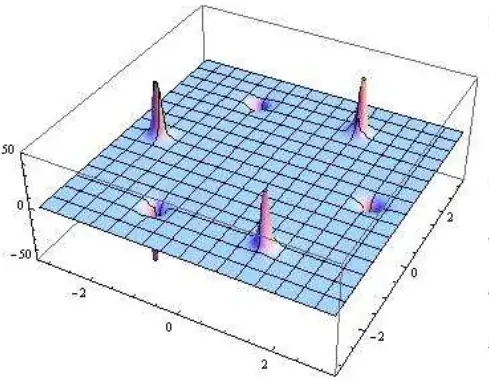
But even for non-TI-symmetric semi-metals, the Berry curvature turns out, in concrete examples, to be strongly concentrated (spiked, see the figures below) around the nodal points, meaning that it tends to effectively vanish away from the nodal points (eg. [Yao+92, Fig. 3] [WYSV06, Figs. 3,6] [FPGM10, Fig. 1] [YXL14, Fig. 1] [Van18, p. 206]).

The following cartoon picture of the situation may help convey why this seems to be remarkable:

enter image description here

Is this concentration of Berry curvature around nodal points understood on general grounds?

In [SF15, p. 3] (more recently repeated in [ZNT21, p. 1]) it says, broadly and without any reference:

Berry curvature often concentrates in small regions in momentum space where two or more bands cross or nearly cross.

What's the status of this statement? What is "often"? Is there a more authorative or at least more comprehensive reference for this general phenomenon?

$\;$

References:

  • [FPGM10] J. N. Fuchs, F. Piéchon, M. O. Goerbig, G. Montambaux: "Topological Berry phase and semiclassical quantization of cyclotron orbits for two dimensional electrons in coupled band models", Eur. Phys. J. B 77 (2010) 351–362 (arXiv:1006.5632, doi:10.1140/epjb/e2010-00259-2)

enter image description here

enter image description here

enter image description here

  • [Yao+92] Y. Yao, L. Kleinman, A. H. MacDonald, J. Sinova, T. Jungwirth, D.-s. Wang, E. Wang, Q. Niu: "First Principles Calculation of Anomalous Hall Conductivity in Ferromagnetic bcc Fe", Phys. Rev. Lett. 92 (2004) 037204 (doi:10.1103/PhysRevLett.92.037204)

  • [YXL14] F. Yang, X. Xu, R.-B. Liu: "Giant Faraday rotation induced by Berry phase in bilayer graphene under strong terahertz fields}, New J. Phys. 16 (2014) 043014 (arXi:1307.7987, doi:10.1088/1367-2630/16/4/043014)

enter image description here

  • [ZNT21] C. Zeng, S. Nandy, S. Tewari: "Nonlinear transport in Weyl semimetals induced by Berry curvature dipole}, Phys. Rev. B 103 (2021) 245119 (doi:10.1103/PhysRevB.103.245119)
Urs Schreiber
  • 14,227

2 Answers2

8

First, here is a common argument for why Berry curvature "often" concentrates at points where bands nearly cross. The (Abelian) Berry curvature of the $n$th band may be written (Eq. (1.13) in your [XCN10]) $$ \Omega^n_{\mu\nu} = i\sum_{n\neq n'} \frac{\left\langle n \middle| \frac{\partial H}{\partial k^\mu} \middle| n' \right\rangle \left\langle n' \middle| \frac{\partial H}{\partial k^\nu} \middle| n \right\rangle - \left( \nu \leftrightarrow \mu\right)}{\left( \epsilon_n - \epsilon_{n'} \right)^2}, $$ where I've opted to make momentum the parameter of interest. Assuming the Hamiltonian $H$ has a well-behaved $k$-dependence, the regions where the Berry curvature can concentrate are controlled by

  1. the energy gap in the denominator, and
  2. whether the numerator vanishes or is non-zero.

Now, this expression is only defined when there is a gap, i.e. $\epsilon_n \neq \epsilon_{n'}$. However, the argument is often extended by analogies to electromagnetism by recalling that Berry curvature is formally similar to a magnetic field in momentum space.

In the case of Weyl semimetals, one usually proceeds by considering a linearized low-energy theory about the nodal point, where the Hamiltonian takes the form $H=h(\mathbf{k})\cdot \vec{\sigma}$, and $\vec{\sigma}$ is the vector of Pauli matrices. Working through the math (see [XCN10] Sec. I.C.3 or this answer) one finds that the associated Berry curvature takes the same form as the field due to a magnetic monopole. Since magnetic monopoles act as sources and drains of the magnetic flux, such degeneracy points end up acting as sources and drains of Berry curvature flux. This implies that (in the absence of other sources) the Berry curvature concentrates near crossings. A similar analogy can be made between extended line degeneracies and solenoids ([MS99], [MS04]).

  • [MS99] G. P. Mikitik, Yu. V. Sharlai: "Manifestation of Berry's Phase in Metal Physics", Phys. Rev. Lett. 82 (1999) 2147(doi:10.1103/PhysRevLett.82.2147)
  • [MS04] G. P. Mikitik, Yu. V. Sharlai: "Berry Phase and de Haas–van Alphen Effect in LaRhIn$_5$", Phys. Rev. Lett. 93 (2004) 106403 (doi:10.1103/PhysRevLett.93.106403)
Anyon
  • 2,909
6

To elaborate on anyon's answer, the Berry curvature is often vanishing in a certain limit because of a symmetry, and in this case there are sometimes Dirac points. If we then weakly break this symmetry, eg. with spin-orbit coupling or some other small perturbation (in materials these perturbations are often quite small, order of $meV$ or smaller) then these points will split, leaving some curvature spikes where they once were. The size of the curvature region will be small, controlled by the ratio of the perturbation to the band gap. This process for creating Berry curvature is sometimes called band inversion, because the Bloch states in the upper and lower bands often look swapped compared to the Bloch states elsewhere in the Brillouin zone.

One large class of models with vanishing Berry curvature are those with two sublattices $A$ and $B$ and only hopping between sublattices (no $AA$ or $BB$ hopping). For spinless fermions with one fermion per site, there are two bands and the Bloch Hamiltonian has the form

$$\begin{bmatrix}0 && h(k) \\ h(k)^* && 0 \end{bmatrix},$$

where $h(k)$ is a complex-valued function. It's easy to show this Hamiltonian has no Berry curvature. You can think of it geometrically: this Bloch Hamiltonian only explores the $X$-$Y$ plane of the 3d space of $2 \times 2$ Hamiltonians---it needs to go also in the $Z$ direction to capture some Berry curvature, which points radially out from the diabolical point in the center.

This is the case for instance with hopping on a hexagonal lattice, and in that case there are also two Dirac points. When we add a small next-nearest-neighbor hopping then these Dirac points gap out (by a $Z$ perturbation in the basis above), leaving some Berry curvature near the special points. For more details see https://topocondmat.org/w4_haldane/haldane_model.html

edit: This question is more topical than I thought! Recently some authors called this weak symmetry breaking "quasi-symmetry" (not a great name imo), and wrote about some consequences https://arxiv.org/abs/2108.02279

Ryan Thorngren
  • 8,254