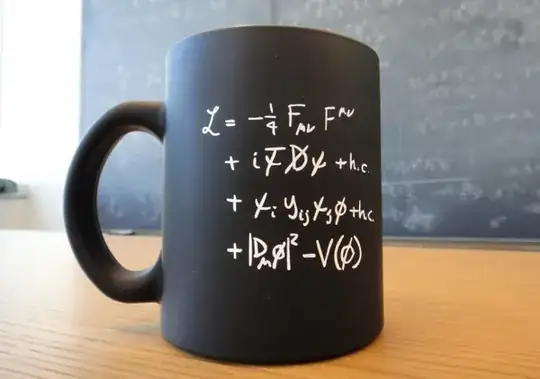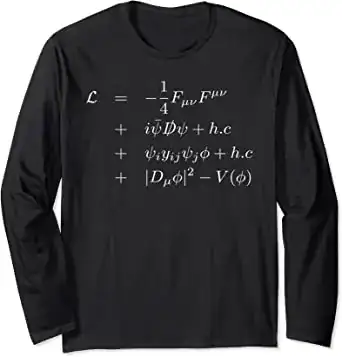A common standard model lagrangian is written in a cup like this. It appears in many places also on a T shirt. But isnt that there is an obvious mistake?
That the Dirac lagrangian is already itself hermitian conjugation.
Thus we only need $$i \bar{\psi} \displaystyle{\not}D \psi$$ instead of $$i \bar{\psi} \displaystyle{\not}D \psi +h.c.$$ on the pictures?