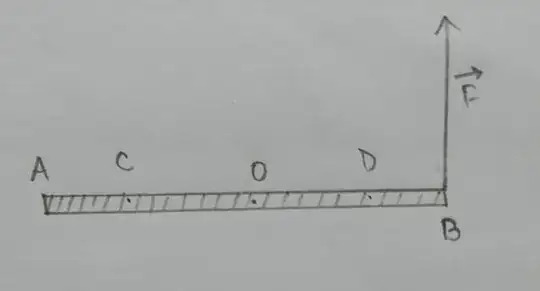
This answer assumes the bar is unconstrained as you stated in your question; specifically, the only forces are gravity down at the center of mass $O$ and $F$ up applied at point $B$ at the right end of the bar as shown in your figure.
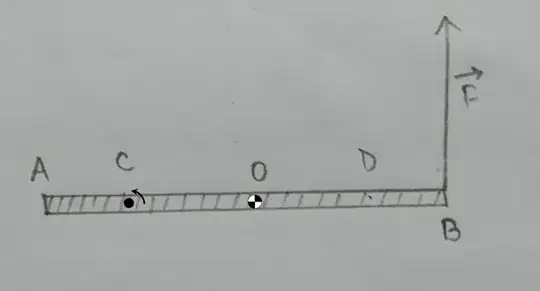
The center of mass of the unconstrained body will accelerate if the vector sum of the external forces, here gravity down and the applied force up, is not zero. The unconstrained bar will rotate with an increasing angular momentum if there is a net torque due to the force of gravity down and the applied force up. Remember that torque depends on the point taken about which the torque is evaluated. For motion of an unconstrained rigid body, the point used for evaluating the rotational motion is almost always taken to be the center of mass of the body, and in that sense the rotation is about the point $O$, the center of mass, in your question.
The translational motion is given by $m\vec a_{CM} = \vec F_{ext}$ where $\vec a_{CM}$ is the acceleration of the center of mass, $m$ is the mass of the bar, and $\vec F_{ext}$ is the net applied external force. Here, $ma_{CM} = F - mg$ where $a_{CM}$ is taken as positive up, $F$ is the force up applied at the end of the bar, and $g$ is the acceleration of gravity downward.
You can describe the rotational motion with respect to any point $Q$ in the body, but this is easiest when $Q$ is taken as the center of mass of the body, in which case (as stated in elementary physics textbooks) $\vec \tau_{CM} = {d \vec L_{CM} \over dt}$, where $\vec \tau_{CM}$ is the net external torque about the center of mass and $\vec L_{CM}$ is the angular momentum about the center of mass; this is true even if the center of mass is accelerating. If $Q$ is not taken as the center of mass, the relationship to be solved is more complicated. See a good textbook on intermediate/advanced mechanics such as Mechanics, by Symon, for the details.
The total motion is best described as: (a) translation of the center of mass with (b) rotation about the center of mass. This motion can be evaluated using the relationships previously discussed.
If the body is constrained, for example by a force keeping the left end $A$ in your diagram fixed, the motion is best described as (a) translation of the center of mass with (b) rotation about the fixed point.
The above discussion assumes that you, the observer, are in an inertial reference frame. If you yourself are accelerating, then fictitious forces and torques must be considered. Again, see a textbook such as Mechanics by Symon for more details.