What is the significance of sliding a force vector?

Question

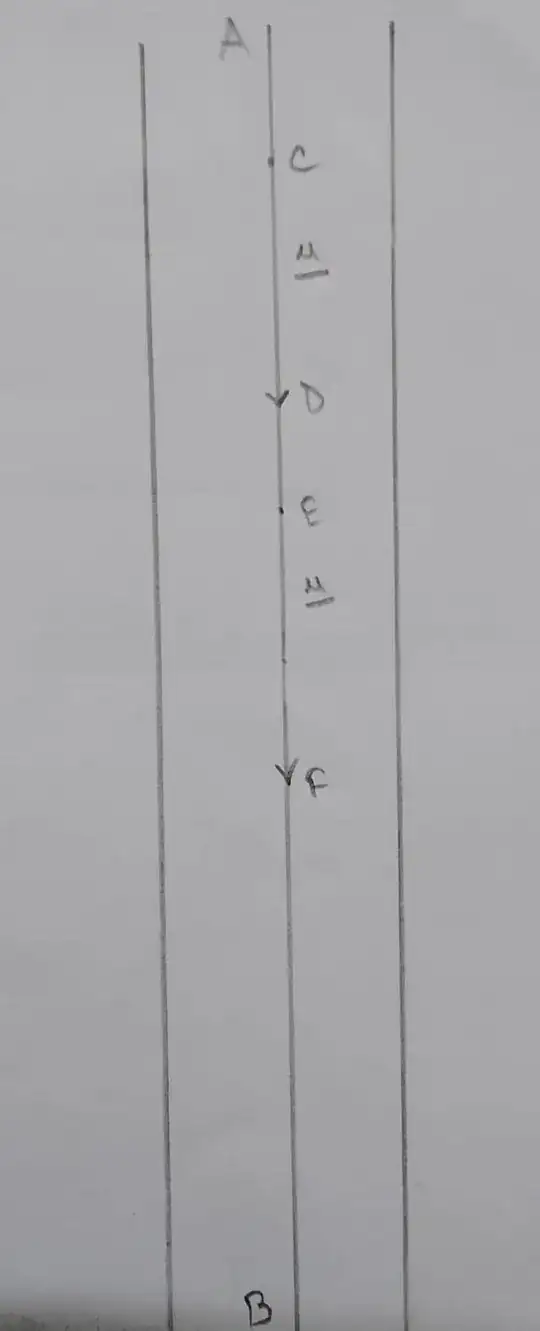
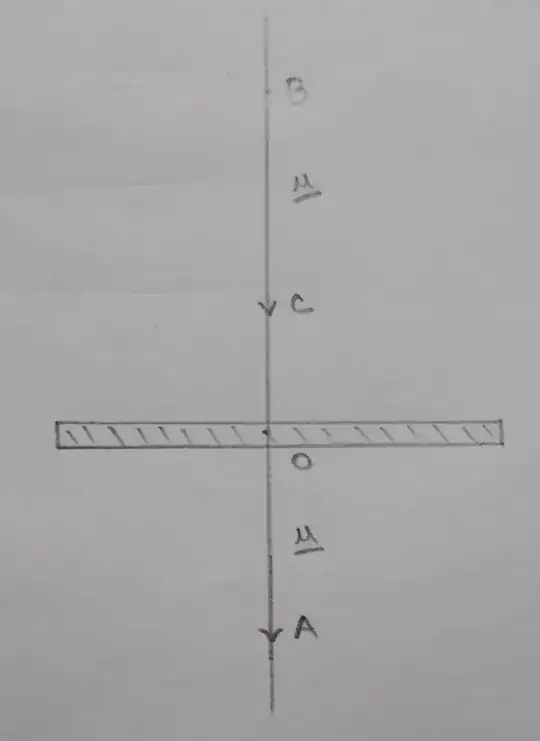
Scenario 1:

Here $AB$ is the line of action of the force $\underline{u}$, and $AB$ passes through the center of mass of an infinitely long rigid and uniform bar. Here, $\vec{CD}=\underline{u}$. Now, if $\vec{CD}$ is slid and $\vec{CD}$ becomes $\vec{EF}=\underline{u}$, the physical effect will remain the same. In other words, it doesn't matter whether the $\underline{u}$ vector acts at the point $C$ or the point $E$, the effect on the bar will remain the same. So, in this scenario, there is utility in the existence of the line of action $AB$.

Scenario 2:

Here $BA$ is the line of action of the force $\underline{u}$, and $BA$ passes through the center of mass of a rigid and uniform bar. Now, let a force $\vec{OA}=\underline{u}$ act at point $O$ of the bar. Now, as force is a sliding vector, we can slide $\vec{OA}$ and $\vec{OA}$ becomes $\vec{BC}$. However, I have a problem here. There is no physical meaning/significance to the vector $\vec{BC}$ as there is to $\vec{OA}$, unlike scenario 1. According to this answer, $\vec{OA}$ can be slid along its line of action, and $\vec{OA}$ and $\vec{BC}$ have the same effect on the bar. However, to reiterate, I believe that there is no physical meaning to $\vec{BC}$ as neither $B$ nor $C$ are points on the bar. $\vec{OA}$ acts on the bar and has a physical meaning since $O$ is a point on the bar. However, $\vec{BC}$ is acting on literally nothing, unlike $\vec{OA}$, so what is the physical meaning of sliding the vector $\vec{OA}$ in this case?

My question:

1. What is the meaning of sliding $\vec{OA}$ in scenario 2?

---

This might help you in answering my question.

Answer 1

Too long to post as a comment.

1. Scenario 2:

   Now, as force is a sliding vector,

   Please carefully read my answer to your previous question, in particular

   3. $\;\ldots$ Here, clearly $\vec F$ and $\vec{OA}$ are “free vectors”.

   and

   The moral is this: after the physical scenario has been mathematically modelled (abstracted), the classification system <free vector versus sliding vector versus bound vector> is unnecessary; instead, carefully respecting the phrasing and conditions of definitions and theorems ensures that steps performed are valid.

2. Scenario 1:

   Here $AB$ is the line of action of the force $\underline{u}$, and $AB$ passes through the center of mass of an infinitely long rigid and uniform bar. Here, $\vec{CD}=\underline{u}$. Now, if $\vec{CD}$ is slid and $\vec{CD}$ becomes $\vec{EF}=\underline{u}$, the physical effect will remain the same. In other words, it doesn't matter whether the $\underline{u}$ vector acts at the point $C$ or the point $E$,

   In this (mathematical) scenario as described,

   • $\vec{CD}$ and $\vec{EF}$ are really the same object;
   • $\vec{CD}$ is not "acting" at any point in particular (its name does not signify that it acts at point $C$)
   • there is no physical effect to speak of (none has been indicated).

Answer 2

You realize that the theory of rigid bodies is an idealization and not reality. A real force not only has a line of action, but also a point(s) of application, and bodies are elastic and not rigid.

Only in the context of this idealization can you really apply the rule of sliding vectors. You can think of mathematical forces vs. real forces. A mathematical force has magnitude, direction, and the line of action because it imparts also a moment of force (torque) about some reference point.

It is this combination of force and torque that fully describes the loading to a system. Any system of forces that produces the same force and torque is indistinguishable from each other (mathematically). The equations of motion are the same.

Mathematical forces do not have an origin point, they are vectors that belong somewhere along the line of action, anywhere would do.

In reality, the reasonable assumption is that a contact force acts somewhere on the surface of the body (where the line of action intersects the body). But other forces may act on different points.

Gravity acts on all particles of the body and thus can be assumed to be concentrated at the center of mass without loss of generality (for rigid bodies).

Buoyancy, aerodynamic forces, magnetism may all have different points where they are acting on away from the center of mass.

But again when dealing with Newtonian mechanics, the point where forces act on does not matter, but the resulting torque about the reference point does. For dynamics problems the reference point has to be the center of mass, but for non-dynamic (statics) problems it can be anywhere.

Answer 3

Firstly Torque is much unlike force. Torque is an origin dependent quantity meaning that it depends on the point you take it around. If someone asks you "calculate the torque?" First question is, about which point?

Compare this with force: For force, you can calculates net force on a body about any point in space and all points will agree. See John's answer here.

There is however one particular special case where Torque becomes a sort of origin independent quantity: When net force is zero. Proof

So, in principle, if you have a body moving in earth, you could set your origin of coordinate system at some point on mars and ask "how much is this body spinning about this point on mars?".

Once, we have all of that out of the way, what does it mean that we can slide the force vector about all those points and the torque is preserved? It's basically an indirect consequence of the fact that when we calculate the torque using the definition $\vec{\tau} = \sum \vec{r_i} \times \vec{F_i}$, how the mass is distributed in space has no relevance for the calculation.