What is the meaning of this statement in Optics, Born-&-Wolf regarding coherence length?

Question

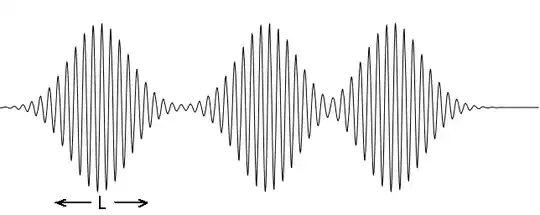
In their treatise "Principles of Optics", Max Born and Emil Wolf state in the section on coherence length (page 317, para 1) that:

...... as the difference of optical path is increased, the visibility of fringes decreases (in general not monotonically), and they eventually, disappear. We can account for this disappearance of the fringes by supposing that the light of the spectral line is not strictly monochromatic, but is made of wavetrains of finite length ...........

I really can't understand what is the meaning of the emphasized line, does it refer of a light pulse of finite length, similar to a pulse going down a string (like the ones we see in video games!) or the width of the spectral line? Please enlighten me!

Answer 1

... by supposing that the light of the spectral line is not strictly monochromatic, but is made of wavetrains of finite length ...

What the authors mean is this.
The wave actually is not an ideal sinusoidal wave of infinite length, like this:

Instead, it is a superposition of wave packets, each

• having the same wavelength $\lambda$,
• a finite packet length $L$,
• and (most importantly) a random position with respect to the other packets.

(The actual shape of the wave packets is not important. I choose Gaussian packets here for convenience. But it could be any other shape of width $L$.)

The result of this feature is that the phase difference between two points of the wave becomes random when they are separated by a distance larger than $L$ (the so-called coherence length).

... does it refer of a light pulse of finite length, similar to a pulse going down a string (like the ones we see in video games!) or the width of the spectral line?

As explained above it refers to light pulses of finite length. But the coherence length $L$ is also related to the width $\Delta\lambda$ of the spectral line by $$L\approx \frac{\lambda^2}{\Delta\lambda}$$