Meaning of the exchange of identical particles

Question

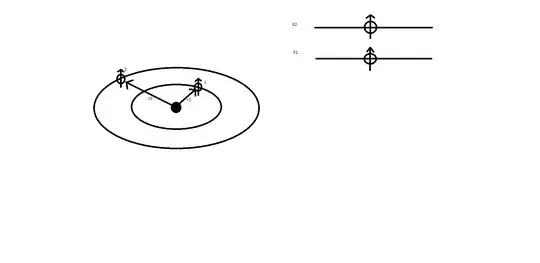
I don't quite understand how the exchange of two indistinguishable particles works. In the image I imagine I have two fermions of spin 1/2 in a kind of Hydrogen atom with two discrete energy levels, $E_1$ and $E_2$. The fermions are non-interacting so the total Hamiltonian is given by the sum of the individual Hamiltonians: $H=H_1+H_2$ and the total eigenfunction is given by $\psi_{\alpha}(\vec{r})=\psi_{\alpha_1}(\vec{r_1})\psi_{\alpha_2}(\vec{r_2})$ where $\alpha_1$ and $\alpha_2$ are the set of quantum numbers of particles $1$ and $2$. From what I know from theory, in the case where the eigenfunction is of the type $\psi_{\alpha}(\vec{r})=\psi_{\alpha_1}(\vec{r_1})\psi_{\alpha_2}(\vec{r_2})$ exchanging two particles means exchanging the set of quantum numbers i.e., if $\hat{C}$ is the exchange operator I have: $\hat{C}\psi_{\alpha_1}(\vec{r_1})\psi_{\alpha_2}(\vec{r_2})=\psi_{\alpha_2}(\vec{r_1})\psi_{\alpha_1}(\vec{r_2})$

Now comes the question:

with reference to my image where the two arrows above the fermions indicate the component along the z-axis of the single particle spin, if I swap the two particles, and from the above this means swapping the two quantum numbers, what do I get? Does it make sense to swap these two identical fermions? I understand that mathematically I get a new eigenfunction using the exchange operator $\hat{C}$ but physically don't I get the same situation as before? That is, a fermion in the $E_1$ level with $S_z=1/2$ and a fermion in the $E_2$ level with $S_z=1/2$? In particular I don't understand what happens when I swap quantum numbers, physically speaking is it like taking one fermion and putting it in place of the other? What does $\vec{r_1}$ mean, is it the coordinate relative to particle $1$? But if the particles are indistinguishable what does it mean to give particle 1 the quantum numbers of particle 2?

Answer 1

Your figure assigns the label 1 to the inner particle and the label 2 to the outer. You could have changed this by assigning label 2 to the inner particle and label 1 to the outer one.

Both drawings represent solutions with the same energy since $E=E_1+E_2=E_2+E_1$ so a linear combination of the two solutions is also a solution. In other words, the properly symmetrized solution is not just “your drawing” but a “linear combination of your drawing plus one where the labels on $\vec r$ are interchanged”.

Which linear combination depends on the total spin state. If the electrons are in a state with total spin $S=0$, and thus antisymmetric under permutation of particle labels, then the “linear combination of your drawings” should be symmetric. If the electrons are in a state of total $S=1$, then the spatial part must be antisymmetric.

As a result, because the spatial part is a combination of two drawings, it does not make sense to think of particle 1 at the inner radius since it could equally well be that particle 1 is on the outer radius.