What is preventing this statement to be true: the twin brother who accelerated away is really decelerating

Question

To summarize the twin paradox: the brother who was in the rocket and flew away is the one having a slower time, because he "accelerated", decelerated and then accelerated again and came back to Earth, while the brother one Earth never accelerated.

But since there is no absolute reference point, can't we say that both brothers on Earth are moving near the speed of light, and the brother who flew away in the rocket decelerated to a speed of 0, and then 70 years passed with this "speed 0" and then he accelerated to come back to Earth. So the brother on Earth was the one having the "high speed (near light)" and therefore the brother on Earth should grow old by 1 year, while the brother that flew away in the rocket have grown old by 70 years? What theory or law is preventing this from being true?

I found the answers so far did not address this:

1. During that 70 years of the rocket twin having speed of 0, his time goes by as usual, so he aged by 70 years
2. The Earth twin has a speed near the speed of light, so his time was really slow. Let's say he aged only by 1 year to see the contrast
3. Therefore, when the rocket twin return to Earth, the rocket twin has aged by 70 years (or more), and the Earth twin by only one year

Specifically, by what law or theory and how does it refute 1, 2, or 3 above?

Answer 1

What theory or law is preventing this from being true?

Nothing prevents the scenario you described. It is, in fact, a completely legitimate application of the principle of relativity.

However, if you work out the actual math you will always find that it is the twin that accelerates that is the most time dilated one. So, although the scenario is valid, your conclusion doesn’t hold.

For example, suppose that in the home twin's frame the trip lasts for 10 years total, and the traveling twin goes out at 0.6 c for 5 years and then immediately turns around and comes back at 0.6 c for 5 years. Then, in the home frame the travelling twin had a time dilation factor of $\gamma=1.25$ so they experience $5/1.25 = 4$ years of time on the outward journey and then $5/1.25 = 4$ years of time on the return journey. At the reunion the home twin aged 10 years and the traveling twin aged 8 years.

In the outward frame the traveling twin is at rest for 4 years, and then must accelerate from 0 to 0.88 c where he will travel for 8.5 years to catch up with the home twin. The home twin travels at a steady 0.6 c for 12.5 years. At the steady 0.6 c the home twin has a steady time dilation of $\gamma=1.25$ so they experience $12.5/1.25=10$ years of time on the total journey. The travelling twin experiences the first 4 years with no time dilation, but during the last 8.5 years at 0.88 c they have a time dilation of $\gamma = 2.125$ so they experience $8.5/2.125=4$ years of time on the second leg of the journey. So exactly as before at the reunion the home twin aged 10 years and the traveling twin aged 8 years.

The scenario you describe is certainly valid, but the actual outcome is not what you had assumed.

Answer 2

Whether the twin accelerates or decelerates doesn't matter- it is still a change of speed, and it is the fact that one twin's speed changes, while the other twin's doesn't, which accounts for the fact that they experience different durations between the moment they depart and the moment they reunite.

To address the specific points you added to the post, you must bear in mind that all the effects of SR are symmetrical between any two inertial frames of reference, and that all motion is relative. If you and I are moving apart at some speed, say 0.5c, it doesn't matter whether you consider yourself to be stationary and me to be moving at 0.5c, or whether I consider myself to be stationary and you to be moving at 0.5c. Indeed, that is the entire point of the principle of relativity.

In my frame time passes normally for me, and in your frame it passes normally for you. However, if you compare the time on your watch to the time on successive clocks you pass in my frame, the time on your watch will fall further behind each clock you pass. Likewise if I compare the time on my watch to the clocks I pass in your frame, my watch will fall further behind as I pass each of your clocks. In other words, my watch will seem time-dilated compared with your clocks, and your watch will seem time dilated compared with my clocks. It doesn't mean that my watch is running slower than your clocks, or that your watch is running slower than mine- what it means is that my clocks are out of synch compared with yours, and vice versa.

In the classic version of the twin paradox, in which one twin moves away from Earth then returns, on each leg of the journey the effects of time dilation are symmetrical- which means that the travelling twin can consider themselves to be stationary and the stay-at-home twin to be moving. What causes the overall time for the travelling twin to be less than the Earth twin is the fact that the travelling twin changes reference frame at the turn around point. There are countless explanations of that on this site and elsewhere, so I will leave it at that.

Answer 3

The point isn't as to who spends more time at low velocity, as you seem to recognize, this is a frame-dependent statement so physical predictions shouldn't depend on it. The point is as to who remains in the same inertial frame and who doesn't. In other words, who accelerates/decelerates and who does neither -- it doesn't matter as to whether the person who doesn't remain inertial accelerated or decelerated. And no matter which frame you choose, you will always see that the brother who remained on earth is the one who always stuck to their inertial frame.

Answer 4

Here's a spacetime diagram to support @Dale's calculation

---

For clarity, I think it's good to clarify some terms.

• Clock Effect. The elapsed time from event-O to event-Z depends on the worldline from O-to-Z. The inertial worldline OTZ logs the longest elapsed time. All other worldlines will generally log different elapsed times, but all are less than OTZ's. (It's the analogue of the triangle-inequality.)
  The real issue is about the spacetime paths between two fixed events (here, O and Z),
  and not so much the "velocities" or "accelerations" used to execute those paths,
  and also not so much about what an astronaut observes about other astronauts.
  It's fundamentally about the paths.
  
  
  
  

• Twin Paradox. Not understanding the fact that
  $$\mathbf {\mbox{ "Being able-to-be-at-rest"} \neq \mbox{"Being inertial"}}.$$ (Although all astronauts can regard themselves as "at rest" [in their own frame],
  not all astronauts can regard themselves as "inertial".
  
  While one can attempt to construct a spacetime diagram where a non-inertial astronaut is at rest and is a straight line on the diagram, that spacetime diagram cannot be obtained by a Lorentz transformation of an inertial astronaut' spacetime diagram. The non-inertial diagram has peculiarities and may not even cover all of spacetime. See Twins Paradox: Why is one frame considered to be the accelerating frame )

Answer 5

So, messing with the first acceleration doesn't matter much because the twins are arbitrarily close-by at the time, you can indeed arrange for the twins to do a relativistic “high five” to coordinate their clocks without stopping the moving twin.

During the constant-speed part of the transport, the twins first see each other's clocks as ticking slower than theirs, then in the second half see each other's clocks as ticking faster than theirs. It is only when they both correct for expected Doppler shift, that they conclude that the other person's clock is ticking slowly. This conclusion is held by both twins.

Side note, acceleration in physics is a vector, so “deceleration” is just acceleration opposite the direction of motion, $\mathbf a\cdot\mathbf v<0$ ... but since the velocity depends on choice of inertial reference frame, whether a given acceleration is a deceleration is not a particularly physical statement.

Ok but now let's talk about that acceleration. It is very important. In fact, I would say it is the most important part of special relativity. The entire Lorentz boost, including the time dilation and length contraction aspects of it, can be derived from the simultaneity shift that is happening during this acceleration.

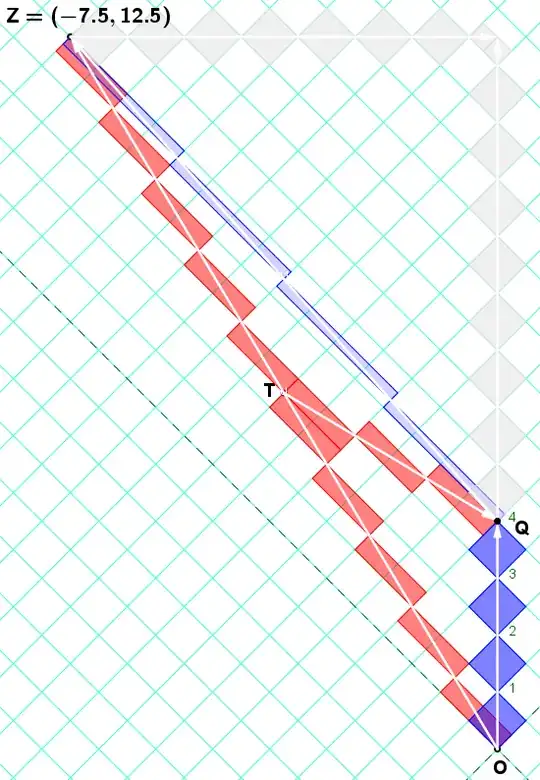
Special relativity says exactly one new first-order prediction about the world, and it is this: when you accelerate towards someone, you see an anomalous Doppler shift due to that acceleration, their clocks appear to tick at the rate $1+ax/c^2$ where $x$ is their distance from you (more precisely: their coordinate in the direction of acceleration), $a$ is your acceleration, and $c^2$ is just some fundamental constant of our universe.

Now you see why the two twins—Alice on the spaceship, Bob on Earth—both see each other's clocks ticking slowly during the inertial parts of the trip, but somehow Alice comes back from her trip predicting/observing that Bob shall be older. Alice literally watches Bob grow dramatically older as she accelerates towards him, she saw him as younger than her, and suddenly he is so much older that even with the return journey's time dilation, he will still look old. And it is because of this combination, Alice accelerates and Bob is a very far distance from her in the direction of her acceleration.

This also gets a little interesting if you freeze it in the context of a periodic universe, where if you travel far enough in some direction you end up back where you started. Because then Alice doesn't just see one Bob, right, she sees in theory an infinite succession of Bobs regularly spaced (albeit she sees older and older light and hence a younger and younger Bob each time, until she sees an Earth before she and Bob were born).