Light traveling in straight lines is an approximation that works very well most of the time. The most common case where it fails is when light travels through a pinhole or slit. Then it bends a little. This is called diffraction.
You can see an example of light bending when you hold your finger and thumb close together as you look between them at your computer monitor. When they are separated, light goes straight from the monitor to your eye. As they nearly touch, a dark bump seems to grow from your fingers to fill the gap. What is really happening is light that was headed toward your eye is bent away.
It happens all the time, but most of the time, the effect is too small to notice. It sometimes matters when people want to be very precise about where light goes.
One place this matters is in camera lenses. They are designed to bring all light that comes from one point of an object to one point on the sensor. If they don't come to a perfect point, the image is blurry.
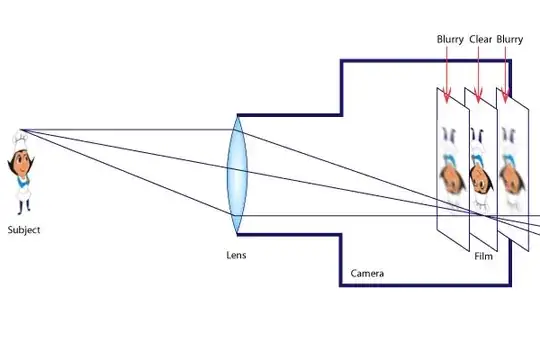
Image from Pass My Exams
A lens is a giant pinhole. A big pinhole causes less bending than a small pinhole. But for a really good lens, diffraction is the biggest reason the focus isn't perfect.
Another place it can matter is in a laser beam. People may want a perfectly cylindrical laser beam that never spreads out. Most beams are pretty close, but they do spread over distance. The rays follow a nearly straight hyperbolic path. This kind of beam is called Gaussian. Here you see a sketch of the curved wave fronts. The rays show the direction the wave fronts travel. The rays are always perpendicular to the wave fronts. The spread is usually a fraction of a degree.
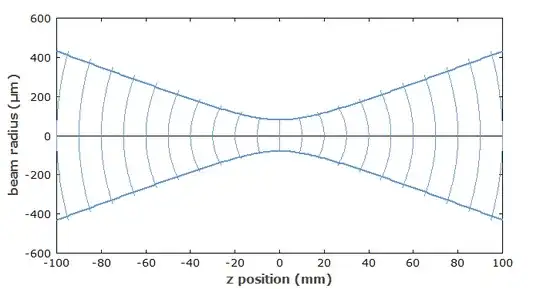
Image from the RP Photonics article on Gaussian Beams
Edit - Responding to comments
The blurring in the out-of-focus planes of a camera is not due to diffraction and is equally well described by the particle model of light.
Good point. The picture does not illustrate diffraction. Perhaps this is confusing. It illustrates that if rays from one point on an object do not hit the same point on the sensor, the image will be blurry. Film or sensor at the wrong distance is one way for this to happen. Lens aberrations are another way of getting rays that do not focus at a point.
Even if these are not present, diffraction will prevent a perfect focus.
A lens causes bending primarily by refraction, and again a particle
model describes this exactly.
Refraction is typically derived from the wave model.
Lens design is usually based on ray tracing and refraction, and typically ignores diffraction. Ray tracing is calculated from the surface radii and indices of refraction of the lenses. The effect of diffraction is usually separately calculated from lens diameters. Diffraction is typically treated as a constraint. There is no point to designing a lens where the aberrations are smaller than the diffraction blur circle.
Diffraction can be calculated from the particle model using the uncertainty principle. This is more easily described with a slit. If a particle of light passes through a slit, the uncertainty of the x component of its position the width of the slit. This creates an uncertainty in the x component of its momentum. This means the particle cannot be precisely aimed that the point predicted from ray tracing. Diffraction through a circular aperture is similar, but the calculations is 2-D.
The changing size of a focused beam of light as it propagates is owing to the curved wavefronts, and this is mostly not diffraction. Diffraction is the fact that wavefronts of finite width cannot avoid some spreading even when they are collimated as much as possible.
There is more to a Gaussian beam than the curved wavefronts. The beam cross section has a Gaussian intensity profile. It is brightest in the center, fading away without reaching $0$. This is not exactly like passing through a pinhole, but the non-uniformity is the cause of the curved wavefronts. This is properly described as diffraction.
The picture illustrates what happens when a beam is focused with a lens. Given a good lens, diffraction determines the spot size, and therefore how much that spot is heated. But exactly the same thing determines the angle at which a collimated beam spreads. The picture would be the same except for a larger beam waist and shallower divergance angle. Either way, the rays are hyperbolic.
As an aside, there is an intensity profile with a Bessel function distribution that is perfectly collimated. This can approximately be achieved by passing a Gaussian beam through an axicon lens. This has applications in drilling operations.

