if $j=l+s$, then I get $1+1/2=1/2$, which doesn't make any sense.
Yes, worded this way it doesn't make sense.
It seems you have misunderstood something.
When you have two angular momentum momenta (with $l$ and $s$),
then these can couple to give states with several different
total angular momenta ($j$):
- The largest possible value is $j_\text{max}=l+s$,
- the smallest possible value is $j_\text{min}=|l-s|$.
- and also the $j$ values in between (with step size $1$) are possible.
Summarizing this you have
$$j = l+s,\ l+s-1,\ l+s-2,\ ...,\ |l-s|.$$
For your example ($l=1$ and $s=\frac{1}{2}$) this boils down to
just two possible values of $j$:
$$j = \frac{3}{2},\ \frac{1}{2}.$$
You can visualize these two groups of states like this.
When $\vec{L}$ and $\vec{S}$ are nearly parallel then you get
the longest $\vec{J}$ ($j=\frac{3}{2}$). When they are nearly
antiparallel then you get the shortest $\vec{J}$ ($j=\frac{1}{2}$).
And for every $j$ there are $2j+1$ different states, from $m_j=+j$
(i.e. $\vec{J}$ pointing up) to $m_j=-j$ (i.e. $\vec{J}$ pointing down).
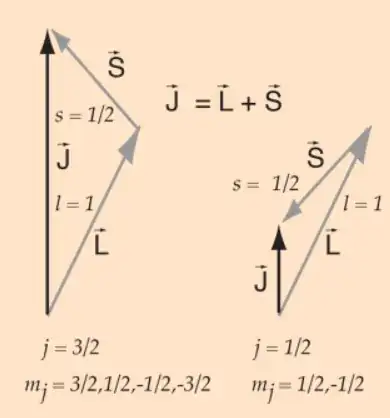
(image from Hyperphysics - Russell-Saunders or L-S coupling)
The $2$ states with $j=\frac{1}{2}$ are
(taken from Angular Momentum in the Hydrogen Atom
where this is worked out in detail):
$$\begin{align}
\left|n=2;l=1;j=\frac{1}{2};m_j=+\frac{1}{2}\right>
&=\sqrt{\frac{1}{3}}\left|n=2;l=1;m_l=0;m_s=+\frac{1}{2}\right> \\
&-\sqrt{\frac{2}{3}}\left|n=2;l=1;m_l=+1;m_s=-\frac{1}{2}\right> \\
\left|n=2;l=1;j=\frac{1}{2};m_j=-\frac{1}{2}\right>
&=\sqrt{\frac{2}{3}}\left|n=2;l=1;m_l=-1;m_s=+\frac{1}{2}\right> \\
&-\sqrt{\frac{1}{3}}\left|n=2;l=1;m_l=0;m_s=-\frac{1}{2}\right>
\end{align}$$
