From the Heisenberg's Uncertainty Principle for position and momentum we know that, $x$ and $p$ of a particle cannot be measured simultaneously with arbitrary accuracy.
$$\Delta x \Delta p \geq \hbar/2 $$
How does the uncertainty principle work in the following experiment?
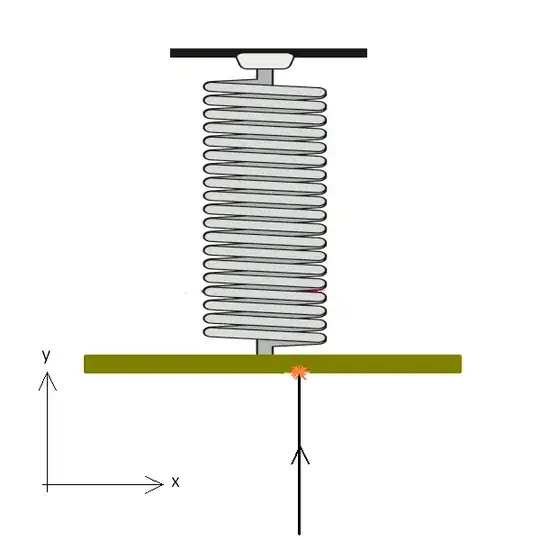
Consider an electron hitting a fluorescent screen which is mounted on a very sensitive (hypothetical) spring. When the electron hits the screen, we know its position at the instant of it hitting the screen. Besides this, it imparts momentum at the instant of hitting the sunscreen which can be calculated from the compression of the spring. Thus getting both position and momentum simultaneously.
What part of the above experiment am I confused about that gives me this wrong conclusion?