When the earth is orbiting around the sun, it experiences a force vector pulling it towards the sun, which acts as a centripetal force for its elliptical orbit. However, when the earth moves a bit from a given position, wouldn't it take time for the information that it's in a new spot to travel to the sun, thereby delaying the direction of the force vector by approximately 8 minutes?
2 Answers
In the Newtonian framework, the force acting on Earth now reflects the position of the Sun $8$ minutes ago. When the Earth takes a little time to move a little bit, the new force acting on it reflects the position of the Sun a little bit less than $8$ minutes ago.
Edit - After David Hammen's comments, I read Speed of gravity. I need to expand on the answer above.
In the Newtonian framework, the Sun creates a gravitational field that exerts a force on Earth towards the Sun. If the Sun is at rest in an inertial frame, the field in that frame is unchanging. As the Earth moves around the Sun, it moves into a location where the field is the same now as it was $8$ minutes ago.
You can also look at this from an inertial frame where the Sun moves at a constant velocity. The Sun and its field are now moving together. If you look at the field along a trajectory that follows the Sun, staying a constant distance and angle from the Sun, the field does not change. If the Earth moves through a point along that trajectory, the field is the same as it was $8$ minutes ago.
You could say the same thing about the E field of a charge. An orbiting charge would see a constant field.
Newton thought that the speed of gravity was infinite. We now know that it is not. It is same as the speed of light. It doesn't matter what the speed is, so long as the Sun or charge doesn't accelerate.
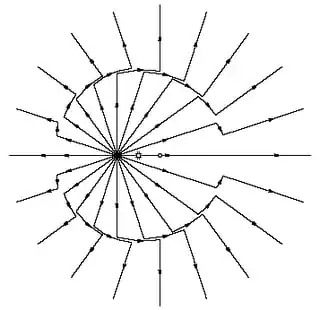
The speed does matter if the Sun or charge does accelerate. You can see an explanation at Why does an accelerated charge radiate away energy?. It includes this picture of what happens if a charge is given a sudden bump.
The field radiates outward at the speed of light. It takes a while for the change to reach an orbiting body. For Earth, it would take $8$ minutes.
The best description of gravity we have is given by General Relativity. See A new way to visualize General Relativity by ScienceClic for a description of GR and how it differs from Newtonian gravity.
Gravity is more complicated than E&M. The picture above shows the idea. But to get correct answers of how gravitational waves behave, you need to use General Relativity.
For everyday use, Newtonian gravity gives almost exactly the same result. But the tiny differences are sometimes important. For example, GR shows that time runs a tiny bit slower at the surface of the Earth than it does in orbit where GPS satellites are. GPS depends on incredibly precise timing. GPS receivers would not work if they did not correct for for this in software.
In astronomy, the most famous difference is in the orbit of Mercury. Newtonian gravity predicts that a one planet solar system would have a perfectly elliptical orbit. GR predicts a very slightly different orbit. It is an ellipse where the long axis slowly changes direction. In a century, it changes by $43$ arc seconds, or about $0.01$ degrees.
Note that if you were planning the trajectory of a rocket from one planet to another, you might need to take the speed of gravity into account. Planets are accelerated by the gravity of the Sun. But there are other effects, such as gravitational time dilation and distortions of distance. If you need such an accurate trajectory that these tiny differences matter, you would need to use General Relativity.
I also read the Scholarpedia article Stability of the solar system. It describes how people have tried to determine if the orbits of the planets are stable ever since Newton. This is not an easy problem. The planets all pull on each other a little. The orbits are always very close to elliptical, but the ellipses slowly change. It isn't clear how these perturbations add up over millions or billions of years.
In recent years, computers have helped. It turns out that if you run two simulations with tiny differences in initial conditions, the differences between the simulations grows. In the long term, the solar system is chaotic. The best efforts so far can predict the evolution out to $10$ million years with an accuracy of a few km. But after $100$ million years, errors in Earth's orbit might be $150$ million km.
People have developed ways to make progress in spite of this. They run many simulations and take averages. They look for patterns.
Using simulations with Newtonian gravity, it works out the the orbits of the inner planets can change back and forth between nearly circular and rather elongated. They can get so elongated that orbits can overlap, leading to collisions. Running simulations over $5$ billion years (the age of the solar system), it works out that a collision will occur $60$% of the time.
On the other hand, if simulations are run with GR, the inner planet orbits almost always stay nearly circular. Collisions occur in $1$% of the simulations.
The solar system we see has nearly circular orbits. This is an indirect confirmation that GR is a better description than Newtonian gravity.
So David is right that the tiny difference between Newtonian gravity and GR does matter for the stability of the solar system. Though I did not see anything that explained if the speed of light delay was the important factor, or if it was the slightly different shape of the orbits.
- 49,702
Newtonian theory is not adequate to answer this question.
The answer from General Relativity for the gravitational problem is like the answer to a similar question in electromagnetism, when one charge experiences the fields due to another charge. In either case it is helpful to focus ones thoughts on two events called the source event and the field event. The field event is some event (a place and time) where we want to calculate the field---for example, the gravitational field due to the Sun (or, if you prefer, the effect on spacetime curvature owing to the Sun). The source event is the event where the worldline of the source (taken here as a point source) intersects the backwards light cone from the field event. For the Earth--Sun problem, the source event is about 8 minutes before the field event in the rest frame of either Sun or Earth. So Earth now responds to the field (or the curvature) caused by the Sun 8 minutes ago. But the interesting fact is that that field (caused by the Sun 8 minutes ago) points towards the location of the Sun now! And this is true no matter which frame you pick!
Take a look at the electric field due to an inertially moving point charge and you get a similar observation. The fields lines point to where the charge is now (in whatever inertial frame you have picked), but that very field configuration was caused by the charge at earlier points on its trajectory.
- 65,285