EDIT: Decided to summarise the lengthy argument below, with a much shorter mathematical argument here. The turning radius of the front wheel ($R_F$) at any instant is given by $$R_F = \frac{L}{\sin \theta}$$ where the steering angle $\theta$ is the angle of the front wheel relative to the rear wheel and L is is distance between the front wheel axle and the rear axle. If the handle bar is held in a fixed position, $\theta$ remains constant and $R_F$ at the next instant remains the same. If the steering angle is continually increased, then the radius of the turn reduces until at the extreme, the front wheel is at 90 degrees relative to the rear wheel and the turning radius becomes $$R_F = \frac{L}{\sin \theta} = \frac{L}{\sin (\pi/2)} = L$$
and the turning centre is now under the rear wheel. The turning centre is never under the front wheel.
========================================
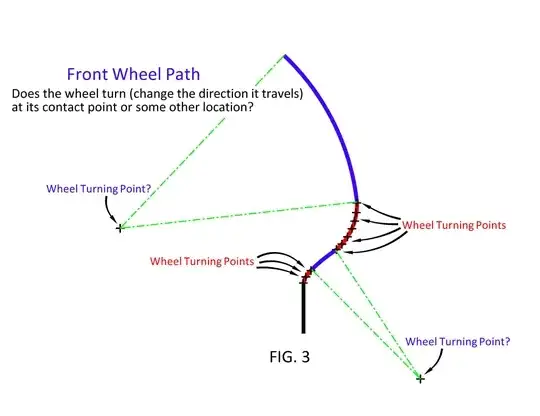
How can the front wheel change travel direction by rotating about its
contact point (red paths) and then mysteriously change the way it
changes its travel direction? (blue paths)
It does not change the way it changes direction.
At any given instant, the front wheel always follows a curve with radius R relative to its instantaneous turning point or centre, where R is the distance from that turning centre.
While the handle bar is turning the wheel, the location of the instantaneous turning centre is continuously changing and while the handlebar is held at a constant non zero angle, the location of the turning centre is constant.
The wheels always follows a path that is tangential to the radii drawn to where their common turning centre is at that instant.
The instantaneous location of the turning centre is always the intersection of the perpendiculars to the tangents of the wheels at their contact point, as depicted in figures 1A to 1D of the original post.
What if, for the red path segments, the wheel was rolling freely - not
attached to the bicycle - and someone was pushing the wheel axle to
make it turn and roll along that red path? Would it then be changing
the direction it rolls as a result of the rotation around a vertical
axis that goes through its contact patch? I would say yes. – Matt Zusy
You raise an interesting point. I guess there is a case for the argument that a wheel that remains upright would turn around a point directly under the wheel if the wheel is being forced to turn by external forces and if the wheel has no forward motion. However, consider the case where the wheel has forward motion and you manually force the wheel to follow a circular path by continually turning the direction the wheel the heading in. That circular path would have a centre and that would be the turning centre of the wheel and it would not be directly under the wheel. There are two separate issues at play here. On is the change in angle of the front wheel relative to the rear wheel as the handlebar is turned and this change in orientation of the front wheel does indeed occur around a vertical axis passing through the contact point, but this is a separate issue to the path followed by the wheel as it moves forward where is has a turning centre that is not under the contact patch.
For a single independent leaning wheel with no external forces, the turning centre is determined by the intersection of the axis of rotation of the wheel and the surface the wheel is rolling on. The more the wheel is leaned over, the smaller its turning radius gets. This can be observed by rolling a tilted coin on a flat surface. It follows a nearly circular path but as it slows down its tilts more and the radius decreases so that its path spirals inwards. In the diagram below, the blue circle shows the path the back wheel follows, if it is not connected to the front wheel and the green circle shows the path the front wheel follows, if it is not connected to the back wheel. They each have independent turning centres (B and F).
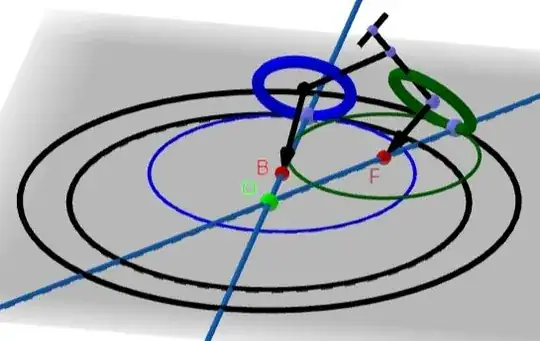
When the wheels are connected by a frame, they are forced to share a common turning centre (O) and its location is determined as described earlier or by simply extending the lines passing through the contact points and the individual turning points to find their common turning point at the intersection of these lines. Now both wheels follow concentric circular paths as shown by the black paths in the diagram.
And when you’re not turning it, how is it turning? – Matt Zusy
If the front wheel is at a fixed angle relative to the rear wheel, then when the bike is pushed forward, the path of least resistance is the one in which the front wheel is rolling around its axle. If you push the bike in a straight line while the front wheel is turned, there is much greater friction between the tyre and the road, than when you let the front wheel follow a path that allows it rotate around its axle.
for instance, what if the (wheel was) rolling freely .. and gravity
was removed. We would think the new wheel velocity direction is
parallel to the wheel plane as the wheel continues to rotate around
the axle. Now quickly turn gravity back on and the wheel starts
turning again.. - Matt Zusy
While gravity is present there is a torque due to the mass of the wheel and there is a gyroscopic reaction torque which causes the wheel to turn and change direction. When the gravity is removed there is is no initiating torque to cause a gyroscopic reaction. This can easily be seen by suspending a rotating bicycle wheel by a string attached to one side of the axle only. The wheel precesses around the vertical axis. When another string is attached to the opposite side of the axle the wheel stops turning around the vertical axis, because there is no initiating torque. Your thought experiment neatly demonstrates that the turning of a front wheel when leaned over in a gravity field, is due to gyroscopic forces.
A vehicle wheel changes direction by forces at its contact patch
only.. – Matt Zusy
We appear to talking past each other. I have mainly been talking about geometry of the path followed by a turning wheel and where the instantaneous centre of that circular path is located. You are talking about the location of where the forces act. These are two different things. In a gravitational field, the forces acting on a free leaning wheel are gyroscopic torque and forces acting at the contact patch. The geometric path followed by the wheel has a radius and centre far from the contact patch.
If you have the skill to ride a bike with holding the handlebars you will notice that when you lean to the right, the front wheel will automatically turn to the right.
Consider when you ride a bike straight and lean it. The wheels do not
turn nor try to turn.. – Matt Zusy
Hold a bike at an angle to the vertical with the wheels parallel to each other and push it forward with no rider. I guarantee the front wheel will turn in the direction of the lean and the bike will follow a circular path. (I used to do this out of curiosity as a kid.) In order for a bike to travel straight while leaned over, a counter weight (e.g. the rider leaning in the opposite direction to the lean of the bike) is needed so that the COM of the combined mass is above the line joining the contact patches. Now the torque due to gravity acting around the horizontal axis is removed and now there is no gyroscopic reaction force, so the bike continues in a straight line while leaned over. (Guess who used to do this as a kid :-)
An additional subtle feature of a turning bike is that the contact patch of the front wheel moves from being directly under the axle when the bike is upright to a point significantly further forward as the bike is leaned over.
This phenomena is described in detail in my answer to "How does tilting a bike make it turn sharper?"
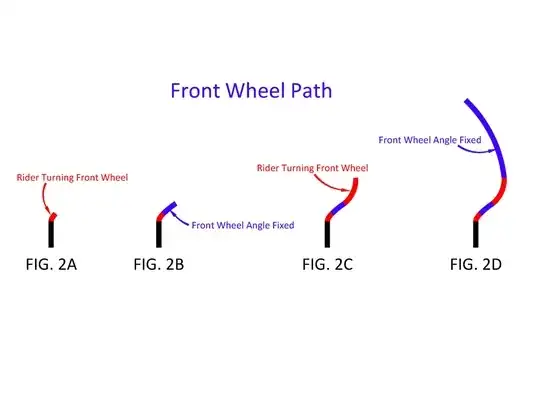
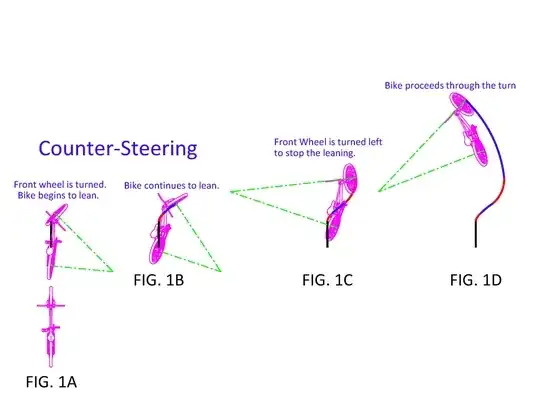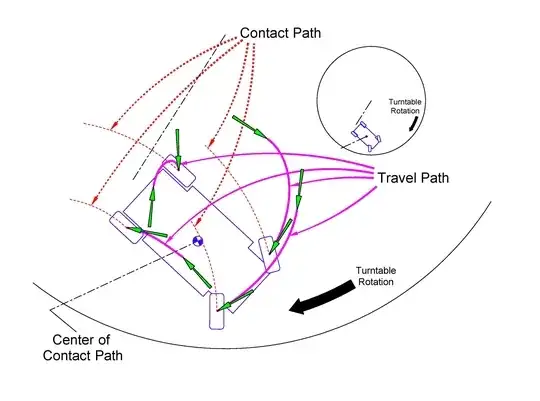
As the bike rolls, there are periods when the rider is turning the front wheel and periods when the rider holds the front wheel at a fixed angle - Figs 2A-D. During the “wheel turning” periods, which are shown in red, the front wheel follows a curved path. Here, the wheel changes direction by rotating/turning about its contact point. Pretty simple stuff because it’s easy to understand how turning a rolling wheel results in curved path travel.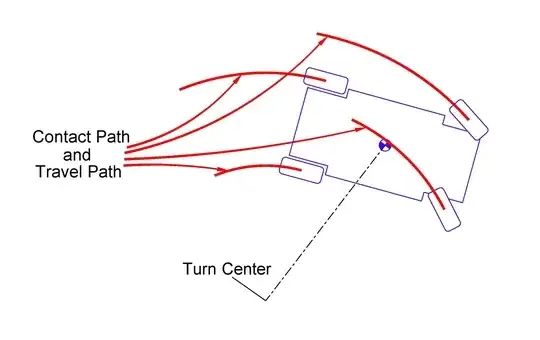
In the next image below: The car corners on the side of a large rotating turntable. The wheels now leave travel paths behind that are not circular. No longer is there a turn center, yet the wheels still leave behind contact travel paths that are circular just as it would when the turntable is still.
