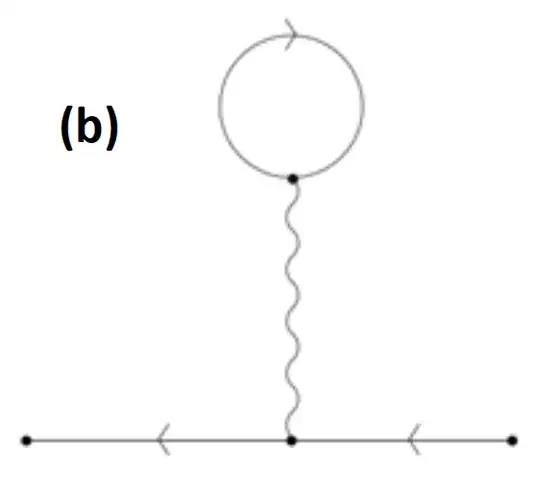
When discussing electron-phonon interaction, the simplest leading electron self-energy usually has only the simplest phonon bubble diagram and excludes the 'tadpole' diagram below with a phonon propagator $D(q=0)$ connected to an electron loop. The argument is $D(q=0)$ should vanish somehow because
the phonon field $\phi(x)$ is a spatial divergence, or
$q=0$ phonon is just an overall translation.
This is what many textbooks say (e.g., page 82 top of Mahan's book (3rd ed.) and page 401 top of Fetter & Walecka's book). But it is not clear to me whether this is only true for acoustic phonons. How about optical phonons? These books seem to only vaguely refer to 'electron-phonon interaction' in terms of this issue.