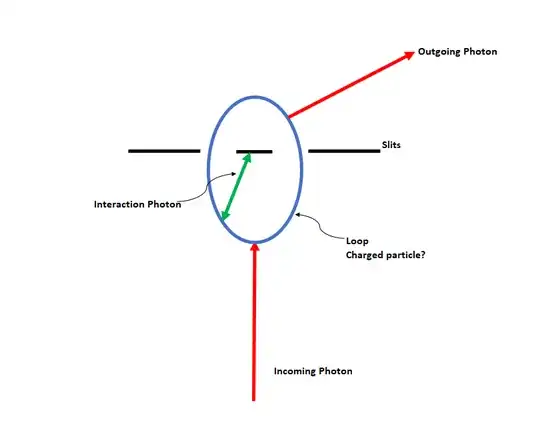
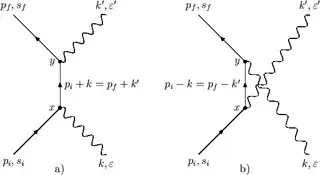
The diffraction pattern is not formed by photons splitting up into pairs of charged particles. Unless the light has a frequency that is high enough to produce electron-positron pairs, the contribution of those virtual loops that are shown in the diagram would be negligible.
To explain the conservation of momentum here, I need to use a bit more technical language. Please bare with me.
We need to say something about the state of the light. Let's start with a single photon state, (a number state with exactly one photon) which we'll denote as $|\psi_1\rangle$. It consists of a superposition (or spectrum) of plane waves. Crudely,
$$ |\psi_1\rangle = |\mathbf{k}_a\rangle C_a + |\mathbf{k}_b\rangle C_b + |\mathbf{k}_c\rangle C_c + ... , $$
where the $\mathbf{k}$'s are the wave vectors of the plane waves and the $C$'s are complex coefficients. More accurately, we can represent it with an integral
$$ |\psi_1\rangle = \int |\mathbf{k}\rangle C(\mathbf{k}) \text{d}\mathbf{k} . $$
We can represent the screen with the two slits as a transmission function $t(\mathbf{x})$. To get the state after the screen, we need to apply an operator $\hat{T}$ that imposes this transmission function on the state. Even if the state before the screen were just a single plane wave, the transmission function would cause the state after the screen to have a spectrum of plane waves. However, the transmission function causes a loss. Therefore, the operator does not maintain the normalization. So, we would need to normalize the state afterward.
To treat the loss correctly, we can model the screen as a beamsplitter that sends the part of the state that is blocked by the screen to a different output port where we can "trace them out." That would give us a mixed state if the original state contained $n>1$ photons (a number state with exactly $n$ photons). In such cases, the interference would be lost.
Fortunately, most experiments are done with laser light, which is represented by a coherent state, instead of a number state. Coherent states remain pure states when they suffer loss. Coherent states are parameterized by spectra, similar to the way we parameterize the single photon state, but in this case, the spectrum is not in general normalized. We'll assume that input state is given by a coherent state $|\alpha\rangle$ with a spectrum $\alpha(\mathbf{k})$.
Now we can use this picture to address the issue of the momentum. The part of the light that passes through the slits is given by $|\alpha'\rangle$ where the spectrum is
$$ \alpha'(\mathbf{k}) = \int t(\mathbf{x})
\exp(i\mathbf{x}\cdot\mathbf{k}-i\mathbf{x}\cdot\mathbf{k}') \alpha(\mathbf{k}') \text{d}\mathbf{k}'\text{d}\mathbf{x} . $$
Note that even if $\alpha(\mathbf{k}')$ was a very narrow spectrum, the modulation with the transmission function will cause $\alpha'(\mathbf{k})$ to have a broader spectrum. On the other hand, the light that is blocked by the screen is given by $|\alpha''\rangle$
where
$$ \alpha''(\mathbf{k}) = \int [1-t(\mathbf{x})]
\exp(i\mathbf{x}\cdot\mathbf{k}-i\mathbf{x}\cdot\mathbf{k}') \alpha(\mathbf{k}') \text{d}\mathbf{k}'\text{d}\mathbf{x} . $$
Note that
$$ \alpha'(\mathbf{k}) + \alpha''(\mathbf{k}) = \alpha(\mathbf{k}) . $$
In other words, the additional components that are present in $\alpha'(\mathbf{k})$ due to the modulation are removed by $\alpha''(\mathbf{k})$ to reproduce $\alpha(\mathbf{k})$. Moreover, for the transmission function we have $t^2(\mathbf{x})=t(\mathbf{x})$, which means that
$$ \int \alpha''(\mathbf{k}) \alpha'(\mathbf{k}) \text{d}\mathbf{k} = 0 . $$
To determine the momentum, we can compute the expectation value of the wave vector. We can do this with an operator
$$ \hat{P} = \hbar \int \mathbf{k} \hat{a}^{\dagger}(\mathbf{k}) \hat{a}(\mathbf{k}) \text{d}\mathbf{k} . $$
It then follows that
$$ \langle\hat{P}\rangle = \langle\alpha|\hat{P}|\alpha\rangle
= \hbar \int \mathbf{k} |\alpha(\mathbf{k})|^2 \text{d}\mathbf{k} , $$
because
$$ \hat{a}(\mathbf{k})|\alpha\rangle = |\alpha\rangle \alpha(\mathbf{k}) . $$
For the light that passes through the slits, we get $\langle\hat{P}\rangle'$ and for the light that is block, we get $\langle\hat{P}\rangle''$, when we use $\alpha'(\mathbf{k})$ and $\alpha''(\mathbf{k})$ in the respective calculations. Based on the properties of these spectra, it then follows that
$$ \langle\hat{P}\rangle' + \langle\hat{P}\rangle'' = \langle\hat{P}\rangle , $$
which shows that momentum is conserved. This happens because the screen receives the momentum of the part of the state that it absorbed.