Why couldn't $s$ and $p$ orbital electrons provide ferromagnetism?

Question

I am trying to figure out why the alkali metals could NOT have Ferromagnetism, unlike iron and cobalt, alkali metals have one valence electron which provides net spin, but why could NOT the alkali metals behave like a magnet?
I understand that according to the Heisenberg hamiltonian for ferromagnetism, if the exchange effect between two electrons is positive, the solid should possess ferromagnetism, but in reality, only a few elements including iron and cobalt possess ferromagnetism.
so why doesn't the $s$ orbital electrons provide the possibility for the solid to possess ferromagnetism?

Answer 1

In magnetism, there are more exceptions than rules. All your rules such as Hund's or the Stoner "criterion" are attempts at formulating indications for collective magnetism. They point in a useful direction but lack predictive power. Even density functional theory simulation struggle with predicting magnetism across wide ranges of materials.

Fe, Ni, Co are far from the only materials that are magnetic. Many alloys and compounds (and even some elements) are magnetic with all kinds of orbitals involved. Many of these compounds contain neither of Fe, Ni, Co, but can often be based on Mn, Cr or rare earths. X-ray magnetic dichroism experiments can be used to judge magnetism on a per element and per orbital basis. In compounds such a transition metal oxides, it is found that even oxygen p electrons contribute spin angular momentum to the total magnetization.

Now for materials made up only of s and p electrons, I don't know what makes it so unlikely for them to achieve sufficient exchange interaction strength. My guess is that low total electron density in these materials makes it less likely for unpaired electrons to end up in an orbital arrangement with sufficient overlap. The more electrons per volume you have, the more likely it becomes. I.e. heavier elements or extreme pressure.

Answer 2

It looks like $p$ electrons can provide ferromagnetism in some cases:

https://www.nature.com/articles/srep08999.pdf , Scientific Reports, 5 : 8999 (2015)

Abstract:

Ferromagnetism can occur in wide-band gap semiconductors as well as in carbon-based materials when specific defects are introduced. It is thus desirable to establish a direct relation between the defects and the resulting ferromagnetism. Here, we contribute to revealing the origin of defect-induced ferromagnetism using SiC as a prototypical example. We show that the long-range ferromagnetic coupling can be attributed to the p electrons of the nearest-neighbor carbon atoms around the $\mathrm{V_{Si}V_C}$ divacancies. Thus, the ferromagnetism is traced down to its microscopic electronic origin.

Answer 3

Alkali atoms all have one valence electron, which detaches from it when the solid metal is formed. The ions left behind have closed shells and thus no net orbital or spin magnetic moment.

The only possibility, therefore, for a ferromagnetic state, is band ferromagnetism, i.e. there must be a splitting of spin up and spin down bands and a transfer of electrons between them leading to unequal populations without, of course, the application of an external field.

The valence bands in an alkali metal are very wide in energy and free-electron like. On the other hand, the d bands in nickel or iron are very narrow in energy.

The exchange interaction will want to align spins and cause an energy splitting between spin up and spin down bands leading to unequal populations. Opposing this is the Pauli exclusion principle which will force the electrons to occupy higher orbitals in the lower energy split band.

Thus the appearance of band ferromagnetism results from the energy gained through the exchange interaction being greater than lost due to the Pauli exclusion principle.

This turns out to be very difficult to attain, and only a narrow band, such as a d-band, has the possibility of this occurring.

A qualitative way to think about this is as follows. If two of the same atoms are brought very close together, you get a diatomic molecule problem and the lower energy state is the one with antisymmetric spins. Many atoms brought together like this leads to wide energy bands and no favorable arrangement that prefers unequal spins populations.

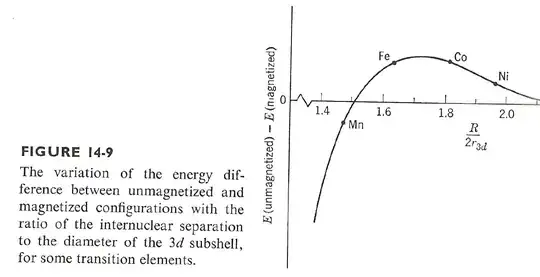
If you begin to increase the separation, overlap of atomic orbitals decreases, the band begins to narrow and look more atomic-like and indistinguishability plays less and less of a role, while exchange plays more and more. If you separate too much, you would expect a paramagnetic response as you have essentially atoms. The plot below, from Eisberg and Resnick in Quantum Theory of Atoms, Molecules, Solids, Nuclei and Particles, shows how the energy of the ferromagnetic state relative the normal state changes as the internuclear separation changes for a 3d state:

We see that too close or too large a separation results in the ferromagnetic state not being the energetically favored state. Fe, Co and Ni are shown to fall into the sweet spot, while Mn does not. To quote the authors:

We see that the ferromagnetic situation is a delicate one in which the valence subshell radius is large enough to permit sufficient space overlap to allow the requirements of indistinguishability to apply, but at the same time small enough to prevent the width of the valence band from becoming too large.

For an alkali metal you would have to have the s band split into spin up and spin down bands and have the exchange interaction favorable enough so that it is energetically favorable to populate the spin up band more than the spin down to get ferromagnetism. But this does not occur because of the large overlap of orbitals and the strong functioning of the exclusion principle. It is just not energetically favorable split the bands and satisfy the exclusion principle and band calculations show this. The only stable solution is the nonmagnetic one.