0

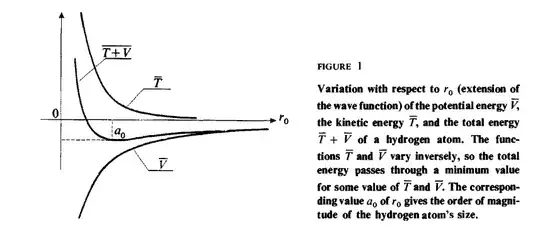
While discussing the stability of hydrogen atom, specifically why the electron falling into the proton won't be the minimum energy state, the reason given is based on uncertainty principle. That the more localized the orbit is around the proton, the more its momentum uncertainty and hence its kinetic energy rises more than the potential energy falls, preventing the total energy to become more negative. Quantum Mechanics, Volume 1 by Bernard Diu, Claude Cohen-Tannoudji, and Franck Laloë provides this graph:

enter image description here

The kinetic energy function due to momentum uncertainty is working similar to a repulsive source in this case.

My question is won't the electron require some force/source of energy/external factor (related to how uncertainty principle works) to prevent itself from permanently falling into the nucleus, since its being attracted by a force (coulombic attraction).

A different (and simpler) example is a gaussian free particle wavepacket. When it is localized, momentum uncertainty is very high and measurements can give a very high momentum/energy value. But as it evolves in time, it spreads in space and (by uncertainty principle) gains a more definite momentum, and very high momentum measurements can't be made now. Clearly, energy is being traded-off for a greater spread in space, even though the particle is free.

This implies to me that naturally particle states tend to "lose" higher energy components. And to make a particle localized, we externally put in some effort (like a single slit or the proton) that provides it with those higher energy components which is what is happening in hydrogen atom. And also happens in single-slit diffraction, as you make the slit narrower, the particles gain momentum in that direction and can appear on the screen very far from the centre.

In essence i am thinking that an external source is needed to prevent particles from spreading completely in space, and this natural tendency of them to spread is what's counterbalancing the attractive coulombic force. I am not sure if this is just a rewording of the uncertainty principle. Any comments are welcome!

Qmechanic
  • 220,844
Deepanshu Bisht
  • 1
  • 2

1 Answers1

1

A proton and electron separately have a total mass-energy of $M = m_p + m_e + U$ where U is the potential energy between them, a negative number.

A neutron has mass-energy $m_n > m_p + m_e > M$

Energy is conserved, so spontaneous electron capture is only possible if the nucleus with n protons and m neutrons has a higher energy of configuration than a nucleus of n-1 protons and m+1 neutrons, which is not usually the case, as such nuclei have decayed already into more stable isotopes.

g s
  • 14,249