Blackbody emission from $N$ parallel & infinite 2D planes

Question

This is something that's been bothering me. A solid object will emit radiation with a flux surface of $\sigma T^4$, but what about a plane?

Here is a thought experiment I came up with to help me make sense of this question:

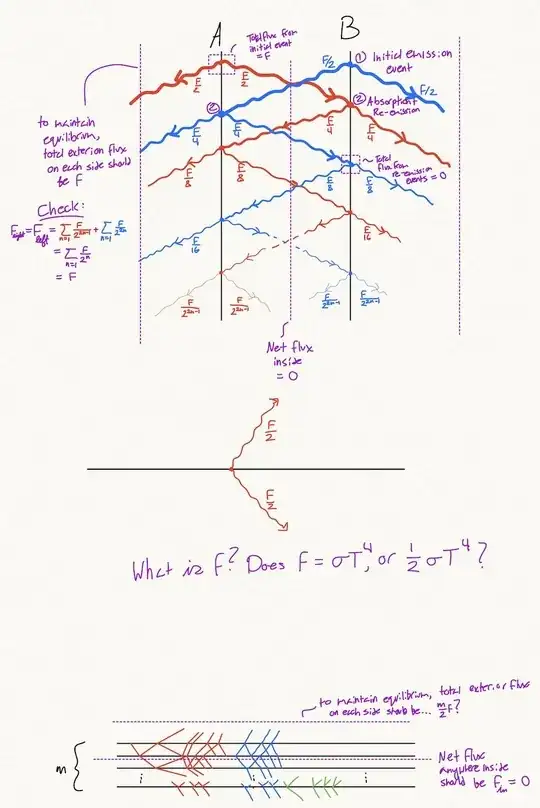
Consider two infinite, parallel planes with zero thickness. They are perfect blackbodies and are at equilibrium with each other and have some constant internal heat source $F$ and have temperature $T$. They both radiate their heat $F = \sigma T^4$ equally in both directions, and immediately do the same for any absorbed radiation that is re-emitted.

Each time a package of radiation is emitted, half of it strikes the opposite plate to be absorbed and then re-emitted in the same way. Summing up the internal radiative flux, we always get zero, no matter the number of absorption + re-emission events. Summing up the leftward flux leaving the left plate, we get that it sums to $F$ after an infinite number of absorption + re-emission events. Conceptually, this makes sense: since the two plates are in equilibrium with each other, there is no net energy transfer between them, so all the energy leaving the system in both directions should total to $2F$.

Now, consider one such plane. The total flux observed through a far-away parallel surface is $F/2 = \sigma T^4 / 2$.

Here are my questions:

• Does it make sense to talk about blackbody emission from something with zero thickness? If so, is my treatment of this system correct? If not, why?

• What about $N$ such planes? Is the total flux observed through a far-away parallel surface equal to $NF/2 = N\sigma T^4/2$?

• More importantly: what does this mean for solid objects, if solid objects (like a solid sphere) and hollow closed objects (like a spherical shell) radiate in the same way? Why do solid objects behave in this way and not like objects with many layers inside of them?

• Are there any real-world objects that behave in this way, such as a single layers of atoms?

Diagram: There are a couple minor typos near the bottom of the diagram. Namely the label $m$ instead of $N$ plates, and $F = \sigma T^4/2$ should read $F = 2\sigma T^4$

Answer 1

There is some ambiguity about what one calls black body radiation: although introductory textbook treatments speak about a "black body" that absorbs all the radiation and so on, what is really meant is radiation (quantum photon gas) in thermal equilibrium. The Planck formula then folows immediately for open space, but the solution may be different when we are talking a region of space with specific boundary conditions - such as a region between two perfectly absorbing planes. Likewise, Stefan-Boltzmann law, referenced in the OP ($\propto T^4$) may not hold in some geometries.

See discussions here, here, and here.

Remark: If the planes are perfectly absorbing, regions between each to adjacent planes can be treated independently, as the radiation does not penetrate through the planes (otherwise they would be partially transparent, i.e., not perfectly absorbing.)

Answer 2

It is unlikely that something that is infinitely thin could be a blackbody, since it must absorb everything incident upon it. It must not allow any radiation to pass through it.

If you observe (from the outside) a sequence of such blackbody planes, then it really does not matter what the "internal structure" is. An external observer sees only radiation from the last surface, with a flux of $\sigma T^4$.

What $T$ is, may well be determined by internal heat sources and structure. In your example you quote $F = \sigma T^4$, and also have an internal heat source $F$, so that to maintain equilibrium, the plane radiates $F$ in each direction.

In your case of $N$ planes, each with an internal heat $F$, then the total flux emitted by the outer planes must be $NF$, with $NF/2$ in each direction.

You will find that there is a problem that the planes cannot all be at the same temperature. There must be a temperature gradient and the radiation from each plane cannot be the same in each direction.