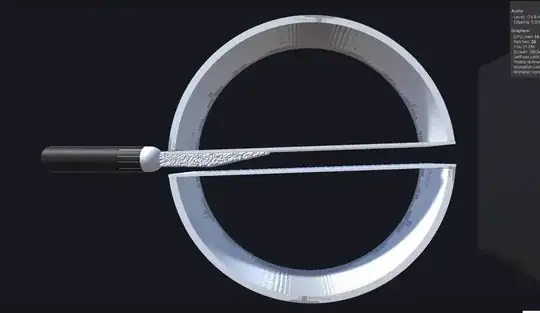
As can be seen in the many creative questions here, it is hotly disputed whether you can measure the speed of light in only one direction to the point where a infamous postulate was made that the speed of light might be instantaneous in one direction; you can never know.
So here is yet another idea that seems to be capable of falsifying above. The question is, what seems to be wrong here / how might the universe conspire?
This is a variation of the original measurement, close to what is described here: Measuring the one-way speed of light?
Instead of a cogwheel we just rotate a path and shine a collimated beam of photons through it. At the end is a flux integrator. The predictions are then:
there should be some rotational speed where no light can make it through the path, if the speed of light is finite.
if the speed of light is finite, the integrator will show a particular shape (amplitude over time) for a particular angular frequency.
expanding on 2, at any given speed you should be able to measure the deviation between an instantaneous assumed speed of light (that will always have the same shape) and the experimentally measured value (which will have start and ends increasingly cut off), thus be able to derive the speed of light.
Of course, if you are able to rotate the device at close to relativistic speeds, you can also derive the speed from 1). But again, the idea is any rotational speed should show a deviation.
Goes without saying the apperatus can be rotated on any axis.
Here's a simulation where the speed of light is slowly increased.
https://www.youtube.com/watch?v=7y-GldVtuVU
Here are two pictures that sort of tell the story from the simulation.