Measuring the one-way speed of light?

Question

I know many people (including me) are bombarding this site with questions about the recent Veritasium video about the one-way speed of light, but I think I found a way.

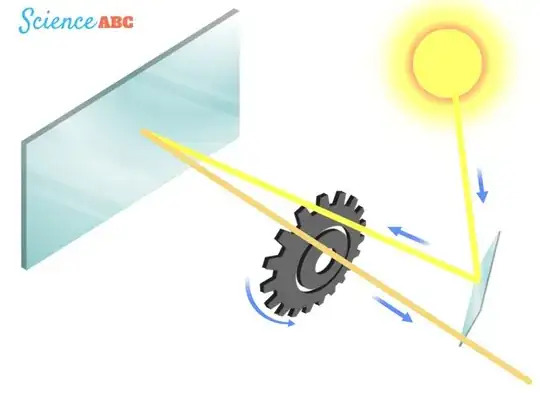
Here it is: (You can see sort of what I am talking about in the picture I attached. Just pretend the mirrors aren't there.)

You could set up a light source and direct it toward a spinning object/wheel with teeth (like the diagram). Then, by adjusting the rotation rate of the wheel, you could see when the light reaches the other side of the wheel/gear (no need to measure how long it takes to get there or back—this eliminates the need for clocks at all [other than any ones need for calibrating the rotation of the wheel]). By knowing the distance the light has to travel to get to the gear, you would be able to calculate its speed if you knew that it passed through the gear at a certain time (based on the rotation rate of the wheel). I know this is very similar to how the speed of light was calculated by Fizeau, but by eliminating the reflection of the light, I believe this setup would work. Am I missing something, or is this possible?

Also, please let me know if my procedure was too incoherent.

Answer 1

This experiment will not measure the speed of light at all, let alone the one way speed (which is impossible to measure without making a simultaneity assumption).

For this specific experiment, no speed is measured at all. We have a spinning gear which alternately blocks and passes light. On the detector side we get a trace that shows that light is alternately blocked and passed. There is no information in that trace that allows us to determine the speed of light. Regardless of the speed of the signal or the length of the path, the trace will be the same.

To turn this into a measurement of speed would require a pair of synchronized clocks so that you can find when the gear tooth blocks the light and when the detector trace shows the light being blocked. Without that additional time information the trace gives no speed information at all. Unfortunately, the usual synchronization process already assumes the one way speed of light is isotropic, which is precisely what we were trying to measure.

In general, any measurement of the one way speed of light will explicitly or implicitly assume some synchronization convention. That assumption determines the measured speed. So there is no way to measure the one way speed of light. Since the two way speed of light is isotropic, it makes sense to use the convention that the one way speed of light is also isotropic, but it is a convention.

Some people think that it is only a matter of adding one more complication to their experiment, but it is not. The definition of the one way speed of light depends on your time coordinates and therefore your choice of synchronization convention. It is not a matter of being a clever experimenter, it is simply a matter of definitions.

Answer 2

I wanted to add this as a comment, but can't because of low reputation, so I will write a bit more.

The experiment is build like this:

light source------------rotating wheel--------------detector

As soon as the rotating wheel is out of the way, the light hits the detector and you measure the time and by knowing the distance get the speed. Do I understand correctly?

I don't think this works. This has the same problem as measuring the speed of light with two clocks (like in the video of Veritasium), but now one clock is exchanged with the wheel. The rotation of the wheel is fixed with a clock and then you move the clock over to the detector. Because the time that is measured in the end is the time difference between the wheel and the clock at the detector. And because of special relativity, this does not work.

Answer 3

I think we can measure one way speed of light. we need to redefine simultaneity. My proposition is as follows: if a rigid body AB of length l is moving without any acceleration parallel to X axis and at time t0 its point A is at location x, then simultaneously its point B is at location x+l

Let's now design the experiment to synchronize distant clocks and measure one way speed of light:

Imagine four spaceships flying as perfect square EFGH towards (or away from) not moving (at least relative to each other) points ABCD, where AD is parallel to EF and distance EF equals AD. Points EG should be collinear with points AB and points FH collinear with CD. Making sure that ABCD (and EFGH) is a square is relatively easy, since 2-way speed of light is constant: we can measure (and correct, if necessary) distances BD and CA by sending light signals from B to D (and from C to A) and back Now we can measure distance from A to G (L) and from D to H (L’) using light (laser) signal send from A to G (and reflected back to A) as well as distance from D to H. If the distance AG (L) equals DH (L’) signals from A and D had been sent simultaneously. Of course the measurements could be done in continuous mode and for example if AG=1000km has been measured at A at 12:00 and DH=1000km at D at 12:15, we would need to adjust the clocks accordingly. Sorry, I could not paste my drawing, but it is simple enough to visualize.

Answer 4

While most approaches to one-way light speed measurement are ambiguous at best there are instances where the assumption that light speed is isotropic is essential to proper operation of the system. The international pulsar timing network is an example and very long baseline radio astronomy interferometry (VLBI) is another. In both of these applications anisotropy of light speed would introduce significant errors. These errors have never been observed. While it is not absolutely conclusive it is reasonable to assume one-way speed as derived from two-way measurements is valid.