Suppose one has a flux of electrons with speed up to 10 m/sec (remark: the speed is not known exactly). The flux which can be modeled as a plane wave (or a semispherical) falls on a net of small openings of the order of 100 nm. The uncertainty of momentum according to Heisenberg Uncertainty Principle HUP is about 70 km/sec. So many of these electrons will have speed above 10 km/sec. What happens here? One can even gain Energy?
3 Answers
What does the HUP mean? It means that in all our experiments in the microcosm of particles, whether creating a beam or sending a beam through definite slits, there is the HUP uncertainty of position versus momentum.
So your beam of electrons already has a HUP uncertainty. They gained this extra momentum to your intended beam momentum while being created into a beam of electrons, the energy provided by the accelerating system.
the order of 100 nm. The uncertainty of momentum according to Heisenberg Uncertainty Principle HUP is about 70 km/sec.
The uncertainty of momentum that can pass the slit system is a filter to the momenta provided by the beam. If the HUP of the beam contains these momenta then some electrons will go through, otherwise no double slit pattern will appear.
- 236,935
Single slit experiment
Most of quantum mechanics in a double slut experiment actually happens at the level of a single slit - the two of them serving only to get a pretty interference picture. Let us therefore consider what happens when a beam or a stream of electrons are directed at a single slit.
A beam of classical electrons
We could consider a classical problem when many electrons fall on a slit simultaneously, with the initial distribution of velocities $p_i(\mathbf{v})$. Most of the electrons are trapped by a screen, but those directed exactly at the slit will pass through, without changing their velocity or energy. Some of them may get scattered elastically by the edges of the slit, that is their energy is conserved. Note that here every electron has a definite velocity and definite energy - the uncertainty is only in their distribution among the electrons. We can then calculate the distribution of velocities on the other side of the screen, $p_f(\mathbf{v})$.
A stream of quantum electrons
Now let us consider a quantum problem, where electrons are incident on the screen one by one, each electron having the same momentum. The essential here is not that they come one by one, but that their initial velocities/momenta are exactly the same, without uncertainty. If the width of a slit is comparable with the de Broglie wave length, the electrons behave like waves. Water in a stream, passing through an opening in a barrage us a good analogy here: we gave plane wave before the slut, but on the other side the wave diverges radially.
The radial divergence is the expression of what @Andrea pointed in their answer: since the slit localizes the electrons in one direction, their momentum in this direction will be uncertain - we can put a detector at any angle in respect to the screen and capture some electrons. Thus, the measured momenta will have some distribution, even though initially all the electrons had the same momentum.
Does it mean breaking of the energy conservation? No. In our classical experiment we implicitly assumed that every electron had a well defined trajectory, a well defined momentum at any point on this trajectory, and a well defined energy related to this momentum by $$K=\frac{\mathbf{p}^2}{2}.$$ The only momeywhen the energy could have deviated from this value was dueing the collision with the edges of the screen.
In the quantum case, the momentum of an electron is defined only when it is measured, but unknown in between. Moreover, the enegy of the electron is now given by $$H=\frac{\mathbf{p}^2}{2}+V(\mathbf{x}),$$ where $V(\mathbf{x})$ is the potential of the screen, which electron, due to its wave-like nature, feels all the time. That is, the energy does not commute with the momentum, and measuring one does not tell us the value of the other - the two variables are also governed by the HUP. The average magnitude of momentum however still has the same value as that of the initial mimentum. And, if we were to measure the energy, which can be viewed as conservation of the kinetic energy.
Remark
Mathematically in the classical example above we would be solving the Fokker-Planck equation for the probability, whereas in the quantum case we solve the Schrödinger equation for the probability amplitude (wave function), and calculate the probability only afterwards as
$$p(\mathbf{x})=|\psi(\mathbf{x})|^2.$$
Energy conservation
Classical mechanics
In classical mechanics energy is the first integral of motion of the equations of motion. If we have only conservative forces, the Newton equations take form:
$$
m\ddot{\mathbf{x}}(t)=-\nabla U[\mathbf{x}(t)]
$$
multiplying this equation by integration factor $\dot{\mathbf{x}}(t)$ we obtain
$$
m\ddot{\mathbf{x}}(t)\dot{\mathbf{x}}(t)+ \nabla U[\mathbf{x}(t)]\dot{\mathbf{x}}(t)=
\frac{d}{dt}\left\{\frac{m\dot{\mathbf{x}}^2(t)}{2}+U[\mathbf{x}(t)]\right\}=0,
$$
from where it follows that quantity
$$
E(t)=\frac{m\dot{\mathbf{x}}^2(t)}{2}+U[\mathbf{x}(t)]
$$
does not change with time, which we refer to as mechanical energy conservation. It is important that this quantity is associated with tracing the change of position $\mathbf{x}(t)$ and velocity $\dot{\mathbf{x}}(t)$ in time, i.e., knowing the trajectory of the particle.
Quantum mechanics
Since in quantum mechanics velocity/momentum and position cannot be exactly measured simultaneously, the above notion of energy conservation in time does not directly apply there.
Ehrenfest theorem The classical equations of motion do apply to the average quantities - the fact that is known as the Ehrenfest theorem. Thus, if we discuss the double slit experiment in terms of electrons incident on a screen one by one, the energy conservation should be understood in terms of such average quantities, as discussed previously. Note however, that the picture of the electrons incident one by one implies that the electrons are wave packets, rather than the momentum eigenstates - that is they have energy and momentum uncertainty even before they reach the slit.
In particular, the average value of energy is given by $$E(t)=\langle \Psi(t)|\hat{H}|\Psi(t)\rangle,$$ where $\hat{H}=\frac{\mathbf{p}^2}{2m}+U(\mathbf{x})$ is the Hamiltonian, whereas $|\Psi(t)\rangle$ is the full wave function obtained by solving the time-dependent Schrödinger equation.
Energy eigenstates The only case where the energy does not have uncertainty is when we are dealing with an energy eigenstate of the Hamiltonian, i.e., the solution of the time-independent Schrödinger equation. However, in this case we have to adopt reasoning in terms of electron waves, which is nearly identical here with the diffraction of electromagnetic waves on a slit.
Let us consider a screen located at $x=0$ perpendicularly to the $x$-axis, with a hole at $y=0$. The electron wave is incident from the left ($x<0$). Following the Huygens principle the solution to the right of the screen can be considered as a radial wave outgoing from the point-like source.
The general Schrödinger equation is (neglecting the direction along the slits for simplicity): $$ -\frac{\hbar^2}{2m}(\partial_x^2+\partial_y^2)\psi(x,y) + U(x,y)\psi(x,y)=E\psi(x,y), $$ where $U(x,y)$ is the potential of the screen and the slit, and $E=\frac{\hbar^2k^2}{2m}$ is the "electron energy" corresponding to a plane wave with momentum $k$ incident from the left of the screen.
For the region $x>0$ we have simply $$ -\frac{\hbar^2}{2m}(\partial_x^2+\partial_y^2)\psi(x,y) =E\psi(x,y), $$ and we look for a solution as a wave diverging from the point $x=0,y=0$ which takes zero value for $x=0$, since the screen is not transparent. It is convenient to pass to the momentum space for the $y$ direction, since this is the momentum which is of interest here: $$ \psi(x,y)=\int\frac{dq}{2\pi}e^{iqy}\phi(x,q). $$ We now end up with the Following Helmholtz equation: $$\partial_x^2\phi(x,q)+(k^2-q^2)\psi(x,q)=0.$$ Its solutions that vanish at $x=0$ are $$ \phi(x,q)=A\sin(x\sqrt{k^2-q^2}), \text{ if } q< k,\\ \phi(x,q)=A\sinh(x\sqrt{q^2-k^2}), \text{ if } q>k $$ The second solution diverges for $x\rightarrow+\infty$ and therefore non-normalizable. We thus arrive at the important result that the transversal momentum is less than the momentum of the original waves incident on the screen: $$q < k.$$ This can be interpreted in terms of energy conservation: a classical particle with momentum $\mathbf{p}=(\hbar k,0)$ when scattered by the slit will have after scattering momentum $\mathbf{p}'=(\hbar\sqrt{k^2-q^2}, \hbar q)$.
If we consider interference picture at the screen located at distance $x$ behind the screen, the distribution of the transversal momenta will be $$ w(q|k, x)\propto \sin^2(x\sqrt{k^2-q^2}). $$ This distribution has zero mean and one can calculate the standard deviation for this distribution as $$ \sigma_q = \sqrt{\frac{\int_{-q}^q dq q^2\sin^2(x\sqrt{k^2-q^2})}{\int_{-q}^qdq \sin^2(x\sqrt{k^2-q^2})}} $$ This is the standard deviation to be used with HUP. However, this distribution has higher moments, and, as we have seen, is bounded to $-k<q<k$. Thus the seeming paradox of the lack of energy conservation when using HUP arises from the assumption that HUP describes a Gaussian distribution of momenta, which is not the case. HUP is too limited to describe more complex distributions (since the mean and the standard deviation form sufficient statistic only for this distribution).
The figure below illustrates the distribution that we obtained:
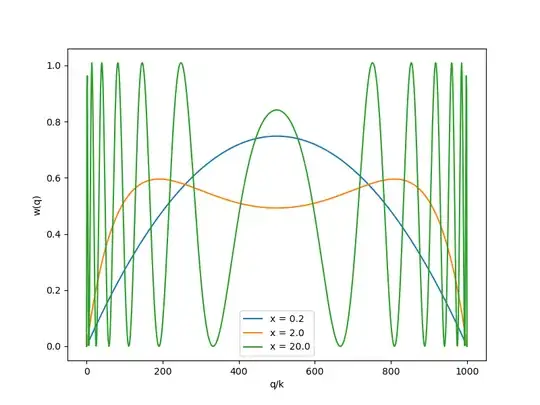
- 68,984
No, diffraction is an elastic process. Energy is conserved, momentum is not.
By diffraction, the parallel (to the 'net of openings') component of momentum can be changed but the total momentum is conserved. Only the direction is changed. The parallel momentum component may even become larger than the total momentum. In this case the perpendicular, say z, momentum becomes imaginary, as $$p_z^2 = p^2-p_x^2-p_x^2 \lt 0 \,.$$ The electron no longer propagates but is extinguished in the z direction.
By the way a more clear description of you grating would help.
- 27,443