Linear wave superposition along a rope/string

Question

This question basically roots to fundamentals of waves which is quite difficult for me to visualize. Hope that I can clear out this confusion based on answers to this question

Would be grateful if someone atleast verifies whether my own answer below is correct or not

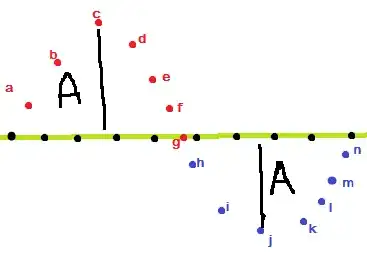
suppose the green line in the image is a string. black dots were drawn to represent particles along the string and the red/blue ones are the displaced(due to wave) particles. Lets say two waves emerged at the two ends of the string and met at the particle $g$. These two waves are of same amplitude and same frequency. Aftermath of this superposition is that all these particles get displaced in the opposite direction nut at equal height after a very small period of time of the meeting of the two waves at $g$ and will move on like that.[All these assumptions are made for a very short period of time. I know that all the particles will return to equilibrium as soon as the energy is transfered completely to succeding particles]

Now the thing I didn't get is the progression of waves even after nullification of waves at $g$. I know that waves aren't nullified but they superimpose in such a way that the particle where they are meeting won't oscillate at all. But how does a mechanical wave propagate? It obviously needs a medium to propagate which in our case is the string. lets say we wanted to create a crest. In order to create that we lifted $a$ at the height of $A$ from the equilibrium position. As soon as we lifted that particle we immediately pulled it down. Now the particles adjacent to $a$ will also get a pull during the lifting but when we pulled $a$ down $b$ didn't go down immediately rather due to inertia it did reach at the height $A$ too. Succeeding particles will face same phenomenon. so to propagate a wave we observed that the preceding particles need to oscillate to transfer that energy to the succeeding ones through attraction, cohesion, adhesion or whatever. But what if a particle isn't oscillating? lets say particle $e$ is hold tightly so that it does not move at all. So it is unlikely that $f$ will oscillate rather it is more likely that the wave will reflect. Will the wave actually reflect back? If it does reflect, how does that reflect?(I can not visualize this one too nor does it seem to me intuitively understandable.) Lets forget holding anything and imagine that the two waves did meet at $g$. Now $g$ won't oscillate since these two waves are at opposite phase. so after the two waves end up at $g$ before the inversion as shown in the video of the link (https://www.youtube.com/watch?v=LJbpXx8fMUk), how does two waves again move from $g$ in two opposite direction? $g$ is supposed to remain static or oscillate but with a very low amplitude, how does it end up evolving waves of higher amplitude?

For this reason I am facing a lot of difficulty in understanding standing waves(how does wave propagate from nodal points if the particle at nodal point itself is not oscillating or is oscillating but with a very low amplitude?). I have looked for many sites for clearing out this confusion but could not find any satisfying answer or maybe I am too dumb to understand.

Answer 1

I was looking for this type of answer. I thought of a way which might answer my own question but do not know whether this thought observation is correct or wrong.

According to above figure I have considered each of these red dots as some designated segments of the rope/string, these pulses are of same amplitude and wavelength. b segment is being pulled upwards by the a segment and downwards by the c segment. And d segment is being pulled downwards and upwards by e and c respectively. There might come a moment when a and e will reach to the equilibrium(gray line) and b and d will reach o the height a. then b will be pulled downwards a and c again d will be pulled upwards by e and c. Now since c is not moving at all this will let b and d to go beyond the equilibrium. If c would have moved this wouldn't have happened, because if c moved upwards then the distance between b and c would have decreased and again at some point this would have increased but at the opposite direction that is c being upwards and b being downwards and would have negated the effect of inertia of b causing it to stop at equilibrium. But c isn't moving so b will move downwards beyond the equilibrium and d will move upwards beyond equilibrium. And this would look as if nothing happened, these two pulses are moving through each other even though they are actually reflecting about c.