Why don't electrons tunnel out of atoms?

Question

The overlap of a free electron wavefunction and a bound electron wavefunction is nonzero. So why don't electrons slowly bleed out of atoms? If any wavefunction enters a free particle state it will just escape!

Answer 1

There are two ways of thinking about this answer. The first is that tunneling allows a particle to pass quantum-mechanically through a barrier that it would not have enough energy to pass through classically. However, this always means tunneling from one classically allowed region to another; the initial and final energies have to be the same. (It is possible, thanks to quantum mechanical uncertainty, to sort of "borrow" enough energy $E$ to pass through the barrier, but only for a short time $\sim\hbar/E$. As $t\rightarrow\infty$, the energy has to be back to the value it started at.) In an atom, an electron is bound, in a negative energy state, while for a continuum/scattering/asymptotic state, the energy is necessarily positive. So there is no tunneling process that can take a bound electron to a free electron. (These facts about the energy have direct experimental consequences in other tunneling processes. In $\alpha$-decay, conceptualized as the tunneling of an $\alpha$-particle out from a positive-energy state inside nucleus, the energy of the outgoing $\alpha$ is related to the halflife, through the Geiger-Nuttall law.)

The second way of understanding this result comes from the consideration of the overlap between the electron wave function in the bound and free states ($|\psi_{0}\rangle$ and $|\vec{k}\rangle$, respectively). If there were an overlap between these two states, then a bound electron could escape into an unbound state. However, in fact $\langle\vec{k}|\psi_{0}\rangle=0$; the two states are orthogonal! That this has to be the case is actually clear from the energy considerations above. The states $|\psi_{0}\rangle$ and $|\vec{k}\rangle$ are both eigenstates of the Hamiltonian $H$, with different eigenvalues (one negative, one positive), so they are necessarily orthogonal.

This may seem confusing, since the Fourier transform $$\tilde{\psi}_{0}\!\left(\vec{k}\right)=\frac{1}{(2\pi)^{3/2}}\int d^{3}r\,e^{-i\vec{k}\cdot\vec{r}}\psi_{0}(\vec{r})$$ is generically going to be nonzero. The resolution of this apparent paradox is that the continuum wave function is not simply a plane wave $\propto e^{i\vec{k}\cdot\vec{r}}$. (In many situations, such as when calculating matrix elements of certain operators between $|\psi_{0}\rangle$ and $|\vec{k}\rangle$, it may be a good enough approximation to use a plane wave for the $|\vec{k}\rangle$ wave function, but it does not work for this calculation.) At large distances, the continuum wave function is close to a plane wave, but in the vicinity of the nucleus [where $\psi_{0}(\vec{r})$ has most of its support], the scattering wave function is strongly distorted by the attractive potential. For a single-electron atom, the continuum wave functions are Coulomb waves; for multi-electron atoms, they are much more complicated, but the qualitative distortion is similar.

Answer 2

You seem to be operating under several misconceptions.

First, quantum tunneling refer to the wave function, not the particle. Second, the description often given for it is a bit misleading. Wikipedia, for instance, says "a wavefunction can propagate through a potential barrier." That makes it sound like the probability mass on the other side of the barrier is increasing. While quantum tunneling can involve changes over time in the probability mass, this is not an inherent feature of the phenomenon. The most basic form of quantum tunneling is a constant (up to phase) wavefunction that exists on both sides of the barrier, no movement from one side of the barrier to the other involved. And even if quantum tunneling involves probability mass moving through position space, it is definitely not a particle moving from one state to another.

Another misconception is that you seem to think that states can transform into others based on their "overlap". This involves a few related sub-misconceptions. First, you seem to think that "overlap" simply means "places in physical space where both wavefunctions have probability mass". Second, you seem to think that particles will spontaneously change from one wavefunction to another.

But in fact the full wavefunction describes how the probability mass changes over both space and time. It's not just a temporary attribute of the particle that is subject to spontaneous fluctuation. For a particle to enter another state, there must be some exterior cause, such as an observation.

Under the wave function collapse interpretation of quantum mechanics, observations cause a particle to enter an eigenstate of the operator associated with the observation (for instance, if the energy is measured, the particle's wave function will collapse to an eigenstate of the energy operator). For each eigenstate, there will be some probability of collapsing into that state, and this probability can be described as coming from the "overlap" of the previous state with the eigenstate, but only if "overlap" is understood to mean the dot product between the states (strictly speaking, it's the projection of the previous state onto the eigenstate, but if all the states have total probability mass 1, then the amplitude of the projection is equal to dot product), not the amount of physical space that the states share.

So, the electron isn't "bleeding" out of the atom. Under most interpretations of quantum mechanics, as long as you're not observing the particle, there's no sense in which it is or isn't outside the atom, so talking about it "bleeding" out of the atom is a bit incoherent. The particle's wavefunction has some probability mass outside the atom, but that probability mass isn't increasing, so the wave function isn't really "bleeding" out either. If you measure the position of the electron, there is some probability of it being outside the atom (where the probability is the dot product of its previous state and the eigenstate of the position operator associated with that position), but as long as the position isn't measured, the wavefunction doesn't change.

Answer 3

The electrons do not tunnel out of atoms, because they are in a potential well with energies below those of the energies of the continuous spectrum. Thinking of tunneling obscures here the basic intuition of energy conservation that we have from classical physics.

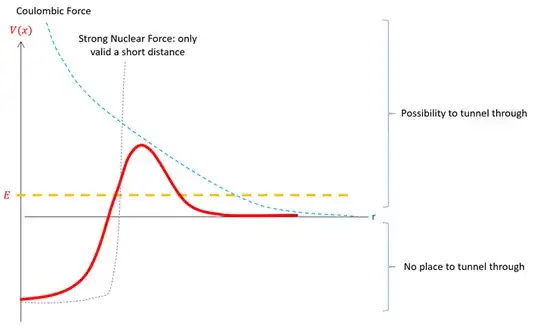
The situation is quite different in radiactive nuclei, where some of the bound states are actually "degenerate" with the continuous spectrum states (see the figure below), and thus tunneling can happen. (It is not quite correct to speak of "degeneracy" here, as in reality the wave functions of stationary states extend beyond the nucleus.)