My book mentions that water contracts on melting, but the book doesn't give any reason why it does so. It is mentioned that:
$1\,\mathrm g$ of ice of volume $1.091\,\mathrm{cm}^3$ at $0^\circ\mathrm C$ contracts on melting to become $1\,\mathrm g$ of water of volume $1\,\mathrm{cm}^3$ at $0^\circ\mathrm C$.
I searched on the internet but I failed to find any useful insight. Could someone please explain why water contracts on melting?
It's because of the crystal structure of the solids. When water freezes, the molecules form various structures of crystals which have empty gaps that cause the solid to be about 9% larger in volume than the liquid was. Metals usually form crystals when they freeze too, but they're often simpler crystals, if you will, and often don't have as much empty space in them as ice/snow does.
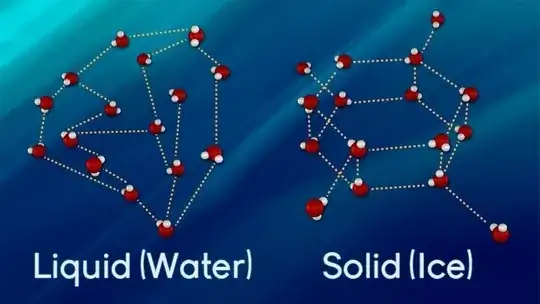
The melting phase transition transforms the long-range ordered-crystalline solid structure into the short-range-ordered average liquid structure. Looking at the process from the solid side, melting can be seen as the dramatic effect of a collective building-up of defects in the solid over a limited interval of temperature, eventually destroying the long-range order at the melting point.
The change of density accompanying the melting can be explained in terms of the kind of dominant defects, and these, in turn, depend on the solid structure. In particular, materials characterized by almost isotropic interactions between the molecules crystallize into compact three-dimensional structures, like the face-centered cubic (fcc) structure. In such a case, the dominant effect of the exponential growth of defects at the melting transition is a sudden decrease of density going from the solid to the liquid.
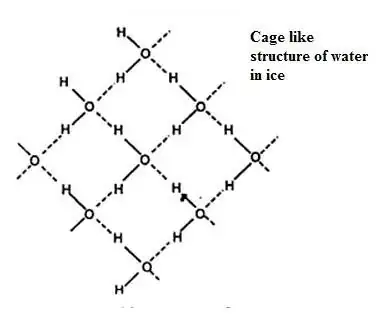
The situation is reversed in materials like water and elements like Bismuth or Silicon, where the molecular or atomic interactions are highly anisotropic. In the case of water, the shape of the molecule, and the important role of the hydrogen bond favor an open structure of the crystal in the same way as the anisotropic interaction between Silicon atoms favors the open diamond structure. At the melting point, the most frequent defects in such open structures induce a local and global collapse of the crystal structure, creating the conditions for a liquid phase at a higher density than the coexisting solid.
In summary, the reason for the increase of density at the melting point of some materials like water can be traced back to the presence of dominant anisotropic interactions favoring open crystalline structure in the solid phase.
You may try to find similarities between water and bismuth, both expand when solidify. Most other materials contract when solidify.
It mostly depends on crystalline structure. Water in form of ice happens to have crystalline structure that takes more space than liquid water.
The structure of ice comes from hydrogen bonds. These occur because the electrons are more strongly attracted to the oxygen atom, so this atom is slightly negative, whereas the hydrogen atoms become slightly positive. You can think of the electrons as spending more time near the oxygen atom. When you put this together with the shallow V shape of a water molecule, the result is that the molecules come together with the hydrogen atoms on one molecule near the oxygen atoms on other molecules.
The resulting structure is not the smallest possible packing for the molecules. Water is denser than ice because in water the molecules can move into positions where there is closer packing as they move around. As the temperature of the water rises to approx 4°C the effectiveness of the hydrogen bonding decreases as the molecules move faster and so the water continues to contract. Above that temperature the speed of the molecules and collisions between them cause expansion, in the same way as for most substances.
Under very high pressures the hydrogen bond forces in ice can be overcome, and other, denser, forms of ice can exist.
The reason is attributed to the hydrogen bonds that determine the structure of ice. The molecules of water in ice are arranged in a cage-like fashion, with rather hollow spaces in between them, thanks to the hydrogen bonds shown as dotted lines:
When ice melts, the energy supplied helps in breaking these hydrogen bonds, and the molecules of water come closer, hence increasing the density of water, or 'contracting it'. This process goes on till the water reaches about 4 degrees Celsius, at which water has the highest density. After this, water expands like any other liquid.
This property has an interesting, but equally important application in nature. As ice is less dense than water, it floats up to the surface of the water bodies and acts as a thermal insulator to the underwater world. This is a boon to aquatic animals and fish during harsh winters.
It also explains other properties of water like the unusually high latent heat of fusion and specific heat.
It has something to do with water being a somewhat unusual compound that is denser and therefore, takes up less space as a liquid than a solid. Greater pressure pushes the material to take up less volume and liquid water takes up less volume than solid water.
If someone wants to give greater detail, feel free, but I think that's the gist of it.
From the thermodynamic point of view, the Clausius–Clapeyron equation should be considered: dp/dT=lambda/[T(V2-V1)]
where lambda is the heat of transformation, p, T and V the usual meanings.
In the p-T phase diagram of pure H2O the equilibrium curve separating normal ice from water has a negative slope and hence dp/dT<0.
When you melt the ice, you must give heat and hence lambda is positive; obviously T>0.
Then (V2-V1) must be negative, that is V1 (ice volume) > V2 (water volume).
Generally speaking, when the equilibrium curve separating the liquid phase from the solid one is dp/dT<0, you have a larger volume in the solid; the reverse for dp/dT>0.
