Is Stellar Aberration a one-way speed of light measurement?

Question

There is a discussion ongoing about the feasibility to measure the one-way speed of light, ever since a Veritasium video on the subject. There is also a wikipedia page about the subject. But Veritasium does not mention Stellar Aberration, and the Wikipedia is funny about it: it has a picture of Stellar Aberration, but does not mention it anywhere in the text.

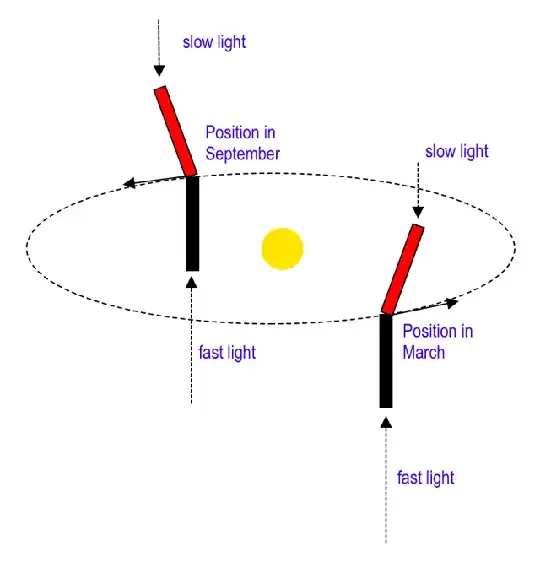
In the following diagram, I have abstracted away the rotation and size of the Earth, and only depicted two telescopes traveling around the Sun. We call the direction orthogonal to the orbital plane "vertical". We simplify the discussion further by assuming there are two stars visible, both exactly in the vertical direction, one far away above the orbital plane, and another one far away below the orbital plane. A (red) telescope is pointing at the upper star, and a (black) telescope is pointing at the lower star.

Due to the limited (one-way) speed of light, and because the telescope is orbiting around the Sun, the telescope must make an angle with the vertical in order to catch the light of a star. That angle is dependent on the one-way speed of light and the speed of the telescope around the Sun. It can be calculated in this simplified case as $tan^{-1}(c_d/v)$ in Newtonian physics, with $c_d$ the one-way speed of light and $v$ the speed of the telescope. In Relativity that becomes $tan^{-1}(c_d/\gamma v)$, with $\gamma$ the Lorentz factor, calculated with the two-way speed of light.

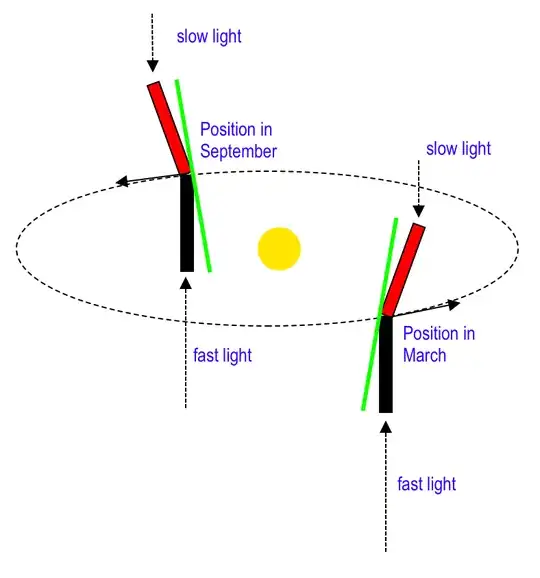
In real life, we don't necessarily know what position a star really has, of course, but we can still compare the aberration angle in March with the aberration angle in September to determine that.

It can be clearly seen from the figure, that if the one-way speeds of the light from the two stars differ, then the aberration angle for them must also differ. If we imagine the extreme case of infinite light speed in one direction, then the aberration angle will be zero for a telescope pointed to that star.

The question been asked before on this forum, but that (more general) question sparked loads of speculative answers, without addressing Stellar Aberration specifically. The one answer by Albert that does address Stellar Aberration, states that it necessarily needs to be based on the one-way speed of the observer:

[...] in addition to the tilt angle of the telescope, one needs to know the speed of the laboratory. But clocks synchronization scheme would affect one – way speed of this laboratory. Hence, as soon as one determines the speed of the laboratory using Einstein-synchronized clocks, the tilt angle of the telescope will indicate that the speed of light is equal exactly to constant c.

But I think we have shown that that is not really true. Even if we don't know the velocity of the observer at all (but it is not zero), if there is a difference in the one-way speeds of light in the two opposing directions, we must see a difference in aberration angle for the two stars. So at the very least we know whether the one-way speed of light in two opposing directions is equal or not, even without knowing the speed of the observer.

And when we determine the speed of the observer, then we determine that speed with the help of clock-synchronisation based on the two-way speed of light in an orthogonal direction. Thus, with the help of that speed, we are comparing the one-way speed in one direction with the two-way speed in an orthogonal direction. That still constitutes a measurement of the one-way speed of light.

So, is Stellar Aberration a measurement of the one-way speed of light, or where is the fault in my reasoning?

Answer 1

We first need to understand that the picture as shown in the question, is an unrealistic view that nobody would have. A real stationary observer outside the solar system would use normal Einsteinian synchronisation of vertical clocks, and would therefore measure an identical one-way light speed in the two vertical directions. This understanding has surprising consequences for which direction can be called vertical in this unrealistic view. To explore this understanding, we first examine the situation from a real observer in a stationary frame.

A real observer in the stationary frame would agree with an astronomer moving with the orbiting telescopes on which direction is vertical; the direction orthogonal to the orbital plane. Suppose the astronomer has positioned a telescope exactly vertically with $T$ its top end, and $B$ its bottom end. The stationary observer places a similar vertical telescope with top $T'$ and bottom $B'$, at rest in the stationary frame. Because both are vertical, it necessarily needs to be the case that the two telescopes are aligned when they pass each other. In other words, the event of $T$ meeting $T'$ and the event of $B$ meeting $B'$ are considered simultaneous in both frames. A measure of simultaneity is that light pulses generated from the $T$-$T'$ and $B$-$B'$ events arrive at the same time at the midpoint $M$ between $T$ and $B$.

As these light pulses arrive at the same time at the same location in the physical frame, they also need to do that in our unrealistic view. In that view, $T$ needs to reach $T'$ before $B$ reaches $B'$, such that the slow light pulse from $T$-$T'$ has more time to reach $M$ than the fast light pulse from $B$-$B'$. That can only happen if the direction that is called "vertical" in the moving frame appears slanted in our unrealistic view. That is, in our unrealistic view, the direction that the astronomers would call "vertical" is the orientation represented by the green lines in the following diagram.

As can be easily seen from the diagram, the astronomers would measure the same angle with the vertical for both telescopes. That is, stellar aberration does not constitute a measurement of the one-way speed of light.