So at 17:38, 3Blue1Brown states:
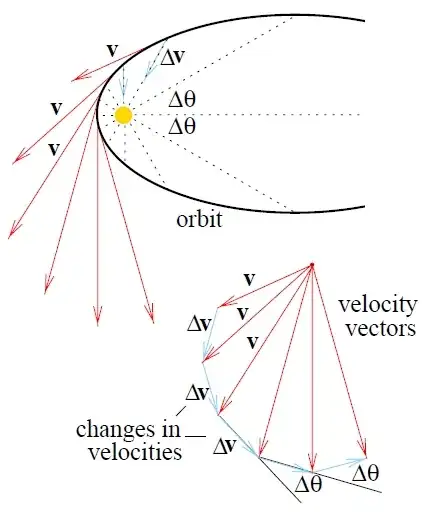
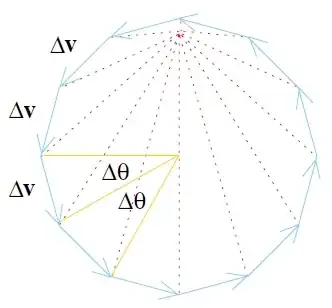
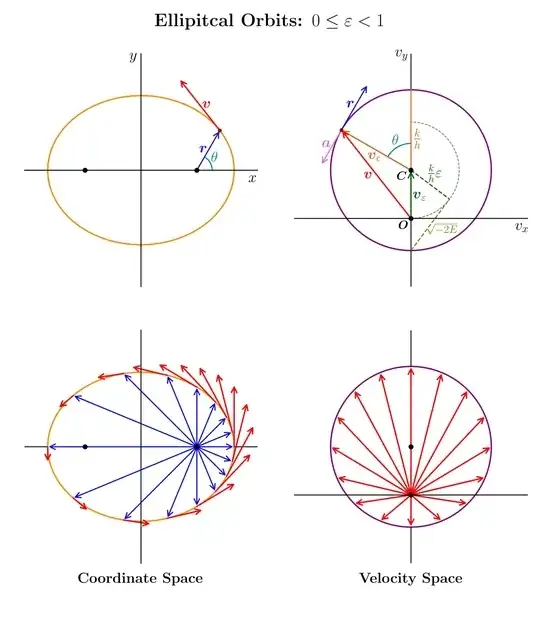
We know that once the planet has turned an angle $\theta$ off the horizontal with respect to the sun, that corresponds to walking $\theta$ degrees around our circle in our velocity diagram, since the acceleration vector rotates just as much as the radial vector.
I'm not sure I quite follow the logic here.
Yes, I can see that the acceleration vector rotate just as much as the radius vector since the sun exerts its force along the radius vector. But what I don't understand is how that translate into saying that the when the position of the planet has turned an angle of $\theta$ with respect to the sun, that means that the "that corresponds to walking $\theta$ around our circle in our velocity diagram", and certainly not how that can be derived from the fact that the acceleration vector rotates just as much as the radius vector.
I think specifically, I'm not sure the meaning of this sentence "walking $\theta$ degrees around our circle in our velocity diagram".