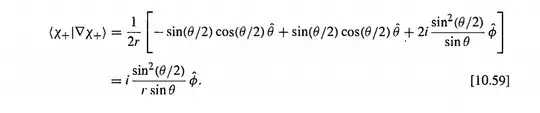A certain field has a singularity at the origin, and the divergence of its curl is zero at any point outside the origin, but surface integral of the curl is not zero in the area of any closed surface containing the origin. So how should the Stokes theorem related to this field be expressed at this time?
1 Answers
The vector field you're considering is $$ \vec{v} = \frac{\sin^2(\theta/2)}{r \sin \theta} $$ If you look carefully, you will notice that this vector field is singular when $\theta = \pi$ (i.e., along the negative $z$-axis.) This means that the curl of this vector field is not defined there either (though its limiting value as you approach the negative $z$-axis is in fact $\hat{r}/2r^2$). And you cannot enclose the origin with a closed surface to perform the integrals required in Stokes' theorem, since your surface cannot include the negative $z$-axis, where the field is undefined.
This vector field, by the way, is better known as the vector potential for the Dirac monopole. This vector field and its nuances have been previously discussed on this site here and here, among other places.
- 54,357