Mathematical description of a conical spacetime

Question

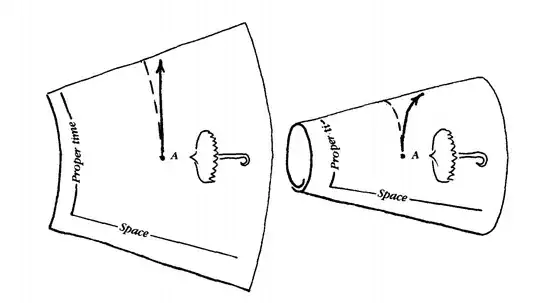
In multiple explanations of general relativity, the curvature of a cone has been used to explain why objects fall in a gravitational field, like so:

It also appears in videos like this and this one from Vsauce.

I am looking for a mathematical description of this conical spacetime. Obviously, the cone describes a flat spacetime, which is to be expected from a uniform gravitational field on the surface of the Earth.

However, I'm struggling to write the metric, because the Euclidean line element for the cone would be:

$$ds^2=dr^2+r^2 d\theta^2$$

I'm not sure if this is the correct metric if time is involved.

I would like to show intuitively that the coordinate acceleration of the falling object is simply due to the choice of coordinates and the corresponding Christoffel symbols.

Also, why does this conical shape correspond physically to a uniform gravitational field? Are there any physical arguments that lead to this shape?

If possible, I'm wondering if there is any link to accelerated frames of reference. For example, does the cone have any connection to Rindler coordinates? I would think that this conical spacetime is an accelerated frame of reference since the surface of the Earth is stationary in these coordinates.

Answer 1

Locally, the metric of a cone is simply Minkowski space (it is most convenient to write this in polar coordiantes). In 3+1 dimensions:

\begin{equation} {\rm d}s^2 = -{\rm d}t^2 + {\rm d}r^2 + r^2 {\rm d} \theta^2 + {\rm d}z^2 \end{equation} However this is not Minkowski spacetime, because the boundary conditions are different. In Minkowski spacetime, $\theta$ is periodic from $0$ to $2\pi$. In a conical spacetime, $\theta$ is periodic from $0$ to $2\pi-\alpha$, where $\alpha$ is the angular deficit.

The form of the metric should make it clear that the curvature is zero everywhere, except for the point $r=0$, where there is a singularity if $\alpha\neq 0$.

There's some more explanation and intuition on this stack exchange answer:

Angular deficit

There is also a nice figure on this page:

https://ncatlab.org/nlab/show/cone+%28Riemannian+geometry%29

To derive the result you want, you would like to draw a curve which wraps around the cone. It is convenient to represent the cone as a flat sheet, with the angular deficit $\alpha$ removed (so your sheet looks like a pizza with a slice removed). The edges of the wedge are identified, so a particle that "hits" the edge on a trajectory that makes an angle $\varphi$ with the wedge, will appear on the other edge of the wedge with the same angle $\varphi$. If you draw pictures of this, you can convince yourself that the net result is that the path is deflected relative to what you would find if the deficit angle were zero.