Why 2nd Shell can have 8 electrons?

Question

I recently watched this video:https://youtu.be/INYZy6_HaQE and understood why 1st orbital can have only 2 electrons: According to Pauli's exclusion principle, two electrons cannot have the same quantum states.In the first energy level,all other quantum states are same except for the spin. And spin can have two values $+\frac{1}{2}$and $-\frac{1}{2}$.So,there can be two electrons in the first shell.

I need a similar explanation for 2nd shell
In other words, why the 2nd shell can have 8 electrons?

I know that there are other quantum states. I am requesting to explain how many values each quantum state can take.For example spin can have two values.Likewise,how many values can the angular momentum can have? How all these lead to the 8 electrons in the second shell? (Don't make it simple,you can use maths.Iam really on to this)

Answer 1

In other words, why the 2nd shell can have 8 electrons?

I do not know just how deep and detailed of an answer you are looking for.
In very simple, not deep at all terms, 2nd shell can have 8 electrons, because 2nd shell has 4 orbitals, and each orbital can have 2 electrons.
1st shell has only 1 orbital, hence 1st shell can have 2 electrons

Answer 2

All the answers you have read so far are models that represent reality as best as possible. The basic starting point is the empirical arrangement of the chemical elements in the periodic table. There we see a periodicity of, 2, 8, 8, 18 and 18 elements (and other higher periods), each ending with a noble gas. The elements are distinguished by the continuous increase of electrons by one electron each. And they are similar for certain numbers of electrons. Good examples are carbon and silicon, fluorine and chlorine or neon and argon.

Absolutely fundamental is the Pauli exclusion principle. It states that electrons in an atom differ in at least one quantum number.

Much less evidence-based are the shell regions, which are defined by the use of special Spherical harmonic. The development of these harmonics was as follows.

1. Periodicity of hydrogen spectral lines.

   It is a fiddle to get a formula for the periodicity of the emission lines of hydrogen. Balmer was the first to succeed in 1885 and Rydberg made an extended formula out of it. All for hydrogen, mind you.

2. Bohrs shell model of atoms

   The first Bohr orbit is filled when it has two electrons, which explains why helium is inert. The second orbit allows eight electrons, and when it is full the atom is neon, again inert. The third orbital contains eight again, except that in the more correct Sommerfeld treatment (reproduced in modern quantum mechanics) there are extra "d" electrons. ... The irregular filling pattern is an effect of interactions between electrons, which are not taken into account in either the Bohr or Sommerfeld models and which are difficult to calculate even in the modern treatment.

   An important piece of the puzzle for Bohr's atomic model was the application of the Rydberg formula.

   In fact, Bohr's derivation of the Rydberg constant, as well as the concomitant agreement of Bohr's formula with experimentally observed spectral lines of the Lyman, Balmer, and Paschen series, and successful theoretical prediction of other lines not yet observed, was one reason that his model was immediately accepted.

   In reality, however, only hydrogen and hydrogen-like elements can be calculated with the Rydberg formula.

   This formula can be directly applied only to hydrogen-like, also called hydrogenic atoms of chemical elements, i.e. atoms with only one electron being affected by an effective nuclear charge (which is easily estimated). Examples would include He+, Li2+, Be3+ etc., where no other electrons exist in the atom.

   But the Rydberg formula also provides correct wavelengths for distant electrons, where the effective nuclear charge can be estimated as the same as that for hydrogen, since all but one of the nuclear charges have been screened by other electrons, and the core of the atom has an effective positive charge of +1.

   Finally, with certain modifications (replacement of Z by Z − 1, and use of the integers 1 and 2 for the ns to give a numerical value of 3⁄4 for the difference of their inverse squares), the Rydberg formula provides correct values in the special case of K-alpha lines,...

   I have quoted this at such length to show the limitation of the Rydberg formula.

Nevertheless, three and later 4 quantum numbers were formed from it.

Some spherical harmonics are shown in the following picture.

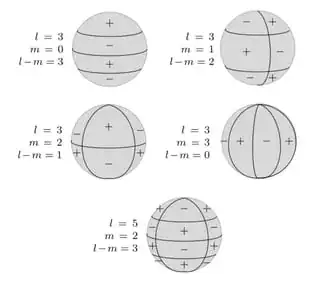
The harmonics on which our picture of the quantised atomic structure is based form lobes along the Carthean coordinate system.

However, there are a variety of other solutions. One of them is shown in the picture in the second row on the left (l=3, m=2, l-m=1).

In this special case, exactly 8 electrons can be calculated. You have to imagine it like a cube, on whose 8 corners the positions of the electrons are located. And it is absolutely amazing that the electron spins can point alternately inwards and outwards for each corner without two nearest electrons having the same spin (corresponding to the + and - signs in the picture above).

Why second shell can have eight electrons?

Because the electron properties together with the nucleus properties give stable situations in nature. The Periodic table of elements is the foundation for any model and the model with 4 quantum numbers is a very complicated model with a lot of exceptions and assumptions that later turned out to be untenable.

Answer 3

If you are a high school student or a freshman yet, I will try explaining in terms you find easy. As you must already know, an electron in an atom has a set of 4 numbers known as its quantum numbers. They are $n,l,m$ and $m_s$. Now these 4 can not be the same for 2 electrons. Let us calculate the number of states possible when we talk about the second shell. We have $n=2$.

Now, $l$ can take values $0$ to $n-1$. Thus here $l$ can take the values $0$ and $1$.

For each $l$ there are $2l+1$ values of $m$ possible which go from $-l$ to $+l$.

Thus when $l=0$ $m$ can be only $0$ and when $l=1$, $m$ can be only from the set $\{-1,0,1\}$.

Taking the above things into consideration you have in total 4 cases for $\{n,l,m\}$

1. $\{2,0,0\}$

2. $\{2,1,-1\}$

3. $\{2,1,0\}$

4. $\{2,1,1\}$

But for each of these the electron can have $2$ values of $m_s$ which are $-1/2$ and $+1/2$. Thus you have in total $8$ combinations of the 4 quantum numbers in the $n=2$ shell. Thus you can't have a 9th electron there because it will have to occupy one of those 8 combinations, which is forbidden by the exclusion principle.

Answer 4

There is no such thing as a "second orbital". There is a second shell which is "made of" four orbitals which each can hold 2 electrons – this is where the 8 comes from.

So there is no contradiction: Each atomic orbital can hold two electrons with opposite spin (according to the Pauli exclusion principle), but there are simply more orbitals in higher shells. The orbitals in one shell have the same principal quantum number $n$, but they differ in the other quantum numbers – the azimuthal quantum number and magnetic quantum number.

For more information, see Atomic orbital and Electron shell.