Is Magnetic force really the relativistic correction for electrostatic force?

Question

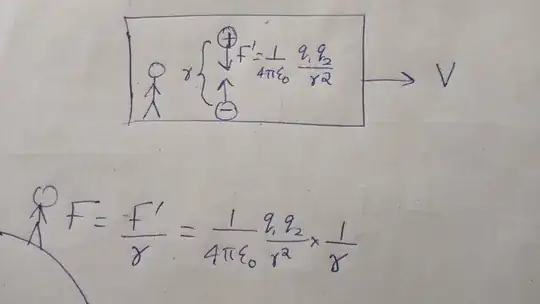
Imagine two charges (aligned vertically) with a separation $r$ in a spaceship moving with a velocity $v$ with respect to earth.

In the spaceship frame, the charges are stationary with a force $$F′=\left(\frac{1}{4πϵ_0}\right)×\frac{q_1q_2}{r^2} $$

If the force between the charges in earth frame is denoted as F, then $$F=\frac{F'}{\gamma}$$

The force is less as seen from the earth frame such that it accounts for time dilation. Many sources say that this reduction is due to the magnetic force which opposes the electrostatic force.

But if we subtract the magnetic force from the electrostatic force, the force as seen from the earth is $$F=\left(\frac{1}{4πϵ_0}\right)×\frac{q_1q_2}{r^2}-\frac{\mu_0}{4\pi}×\frac{q_1q_2v^2}{r^2}$$

simplifying this, we get $$F=\frac{F'}{\gamma^2}$$

But shouldn't it be $F=\frac{F'}{\gamma}$?

Where have I gone wrong? Or is the idea that magnetic force is the relativistic correction for electric force incorrect?

Answer 1

The problem is that you considered an incorrect version for both the electric field and the magnetic field from the standpoint of the observer on the earth. The correct form, according to Resnick, is that the electric field, as well as the magnetic one, is measured to be increased by the gamma factor compared to those measured in the rest frame of the charges. Indeed, you have $E=\gamma E'$ and $B=vE/c^2=v\gamma E'/c^2$. Therefore, you ought to write:

$$F=Eq_1-q_1vB=(\gamma E')q_1-q_1v(\frac{v}{c^2}E)=(\gamma E')q_1-q_1v(\frac{v}{c^2}\gamma E')$$

$$=(\frac{\boldsymbol{\gamma}}{4πϵ_0})×\frac{q_1q_2}{r^2}-\frac{\boldsymbol{\gamma}}{4πϵ_0}×\frac{q_1q_2v^2}{c^2r^2}\space.$$

Then, we have:

$$F=\frac{F'}{\gamma}$$

Answer 2

For the two particles, as seen from Earth, time goes slower while their masses increase. Propper acceleration (about which we talk) is Lorenz invariant.
Now $a=\frac{F}{m}$. Inside the rocket, for each particle, $a=\frac{F_{el}}{m}$. As seen from Earth $a'=\frac{F_{el+mag}}{\gamma m}$. If the force as seen from Earth decreases in the way as the books state, $F'=\frac{F}{\gamma}$, then $a'=\frac{F}{{m\gamma}^2}$. So it seems that $a'$ doesn't equal $a$. But since $a$ is defined as $\frac{dx}{{dt}^2}$ there is a factor $\frac{1}{{\gamma}^2}$ introduced in $a'$ too (as on the right hand side of the expression for $a'$) because $dx$ is the same for someone on Earth and someone in the rocket. So both accelerations are equal as they should be.

So something has to be wrong with your expression. I can't tell you what though.

Is maybe the idea wrong that you can add the electric force and the magnetic force to obtain $F'$? After all, this is a classical calculation that can be done even in the time of Maxwell. I think this is indeed the case. So there is nothing wrong with your calculation by itself, but by its implementation in SR. So you can't use it to derive SR from it.

As I already stated in my comments, seen from the Earth space in the direction of motion of the rocket is contracted. This causes the electric field and magnetic field to be contracted too. The density of field lines increases. Hence the electric and magnetic fields are not how you have written them in the formula you ask about. In a classical view (in the time of Maxwell) your calculation would have been right. But in the context of SR it breaks down. This is in fact what has motivated Einstein. He said that acceleration has to be the same in all reference frames. Note that it not the force that has to be equal in both frames. The force decreases by a factor $\gamma$ while the mass increases by a factor $\gamma$, so the acceleration will stay the same. The fact that your formula doesn't give the same acceleration in both frames

Answer 3

The force between 2 electrons moving parallel at speed V measured as a fraction of the speed of light, is √[1−V²] less than if they were stationary. You can either explain this by saying that due to relativity the electric force is reduced by this factor, or you can say that the electric force remains the same, but there is a magnetic force of 1 − √[1−V²].

The magnetic force between an electron and an infinitely long current-carrying wire, is a different situation. Trying to explain this using just the effect above gives the wrong answer. If you were to assume that the magnetic force between individual electrons was 1 − [1−V²] = V², then you would get the right answer, but that would not be a proper explanation. I think that is the cause of your confusion.

Do not be conned by the other comments and answers, as physics textbooks invariably print nonsense on this subject.