Implications of proper Lorentz transformations having determinant one

Question

I'm presently studying the proper Lorentz transformations of a simple 1+1D Minkowski spacetime. What I know is that the matrices corresponding to those transformations have determinant of +1.

$$ det\left[\begin{array}{cc} \gamma & -\gamma \frac{v}{c^2} \\ -\gamma v & \gamma \end{array}\right] = +1 $$

What I don't know is what this implies in physical terms. Is there any practical reason why areas of a spacetime diagram should remain constant after applying such transformations? Are areas describing any meaningful quantity?

Answer 1

Here is a partial answer to your questions:

Are areas describing any meaningful quantity?

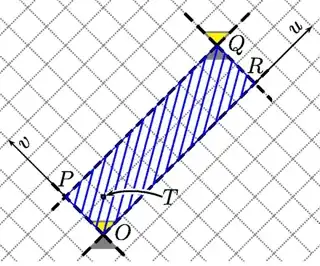
In (1+1)D-Minkowski spacetime, the area of causal diamond of OQ (the intersection of the causal future of event O and the causal past of event Q, where OQ is future causal) is equal to square-interval of OQ (the causal diagonal of the diamond).

This fact is exploited in my article
"Relativity on rotated graph paper"
American Journal of Physics 84, 344 (2016); https://doi.org/10.1119/1.4943251
which tries visualize the ticks (as traced out by a standard-issued light-clock) along piecewise-inertial segments on a spacetime diagram.
(See my entry at also https://www.physicsforums.com/insights/relativity-rotated-graph-paper/ )

(One inspiration of this approach was referenced in the above:
"Space–time intervals as light rectangles"
American Journal of Physics 66, 1077 (1998); https://doi.org/10.1119/1.19047
N. David Mermin)

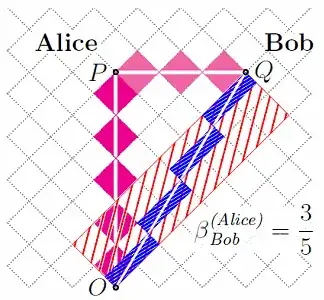
In the diagram below, the area of the causal diamond of OQ is 16 units.
So the square interval of the diagonal OQ is 4.
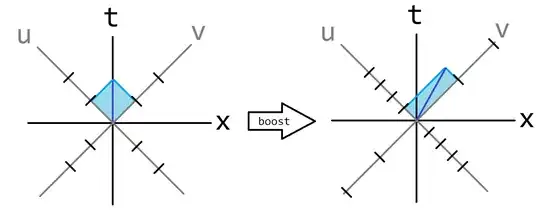
(The diagonal OQ is a segment of a worldline with velocity 3/5c, as seen in the next diagram... where some points are relabeled. Note that all ticks [called light-clock diamonds] along all piecewise-inertial worldlines have the same area.

This follows from the fact that the set of “1 tick events after separation” lie on a hyperbola... which follows from the determinant being equal to 1.)

Answer 2

In $(t,x)$ coordinates, a boost acts as $$ \begin{pmatrix} t \\ x \end{pmatrix} \mapsto \begin{pmatrix} \cosh \phi & \sinh \phi \\ \sinh \phi & \cosh \phi \end{pmatrix} \begin{pmatrix} t \\ x \end{pmatrix}. $$ where $\phi$ is the rapidity (just a more convenient way to parameterize boosts) where $\cosh$ and $\sinh$ are just the "hyperbolic trigonometric functions," i.e. $$ \cosh \phi = \frac{1}{2} ( e^\phi + e^{- \phi} ) = \gamma \\ \sinh \phi = \frac{1}{2} ( e^\phi - e^{- \phi} ) = \gamma v $$ which we use because they satisfy the identity $$ (\cosh \phi)^2 - (\sinh \phi)^2 = 1 $$ just like how $$ (\gamma)^2 - (\gamma v)^2 = 1. $$

Anyway, in lightcone coordinates $$ u = t - x \\ v = t + x $$ a boost acts as $$ \begin{pmatrix} u \\ v \end{pmatrix} \mapsto \begin{pmatrix} e^{-\phi} & 0 \\ 0 & e^{\phi} \end{pmatrix} \begin{pmatrix} u \\ v \end{pmatrix} $$ where to get the above formula we just used the definitions $$ \cosh \phi + \sinh \phi = e^\phi \\ \cosh \phi - \sinh \phi = e^{- \phi}. $$ If you want $e^\phi$ in terms of $v$, then $$ e^\phi = \cosh \phi + \sinh \phi = \gamma + \gamma v = \frac{1 + v}{\sqrt{1 - v^2}} = \sqrt{ \frac{ 1 + v}{1 - v} }. $$ The point is that this transformation elongates the $v$ coordinate while squashing the $u$ coordinates in such a way that the total $uv$ area is preserved.

Note that $$ uv = t^2 - x^2 $$ which is the invariant spacetime interval squared for someone who starts at $(0,0)$ and ends up at $(u,v)$. So the invariance of this area is exactly the invariance of the proper time under a Lorentz transformation, as one might expect.