How to explain this seeming paradox in how the Lorentz contraction, time desychronization, and time dilation fit together?

Question

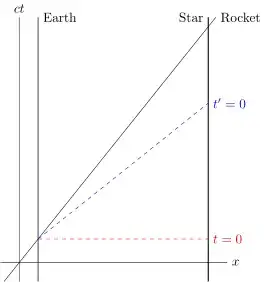
In the earth frame, there is a star ten light years from earth, and at rest with respect to the earth. In the earth frame, a rocket is passing the earth at 0.999999 times the speed of light in a vacuum. In the earth frame the clocks on the earth, star, and rocket all display "zero" at this time.

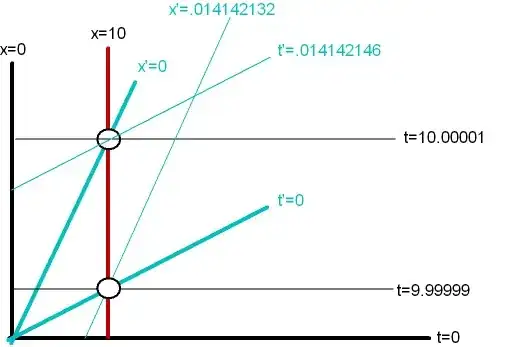
In the rocket frame, the star is (due to Lorentz contraction), (because gamma is 707.1) 5.16 light days from the rocket and the earth, and the star clock displays a little under "ten years", due to time desynchronization. In the rocket frame, the star takes just over 5.16 days to reach the rocket (which regards its frame as being at rest), during which time the star clock changes by a negligible amount, due to time dilation being so great (gamma is 707) and the journey time in the rocket frame being so short (just over 5.16 days). So it should still read less than "ten years".

The trip in the earth-star frame has taken just over ten years, so the clock on the star must read just over ten years when the rocket arrives at the star.

In the rocket frame, when the rocket arrives at the star, the star clock displays just over ten years, because that's how long the trip took in the earth-star frame, and now that the rocket is at the star, the display of the star clock in the two frames are the same.

This is the paradox. In the rocket frame how does the star clock get from just under ten years to just over ten years during just 5.16 light days of highly time-dilated running?

It seems helpful to consider what happens if the rocket makes the trip at a slightly lower speed. The star clock, in the rocket frame, initially displays a quantity that is even further below ten years. The journey time in the earth-star frame is greater than ten years by an even greater amount. But in the rocket frame the star clock still doesn't have a much different chance to advance, due to the combination of Lorentz contraction and time dilation. I mean, the journey now takes maybe 10 days, in the rocket frame, so the star clock will only advance (because gamma is 707.1) about 240 hours divided by say 353 which is about 0.69 hours.

If there are calculations that can disprove my intuitions, I would be glad to see them.

Edit: I don't know how I got 0.69 hours. That might not be right. Maybe it's a back of an envelope calculation gone wrong.

Answer 1

This question is related to your view that clocks 'jump' in the twin paradox- which is a misunderstanding. Observers on the rocket and the Earth disagree about when the star begins its journey.

Consider this analogy. You and I are are timing how long it takes for a climber to scale a distant mountain, the base of which is ill defined. We each look at the climber with a telescope that has a spirit level attached, so that when we see the climber in the centre of our telescopes in the horizontal position (ie level with us), we can take that as the start of the climb. If your spirit level is not adjusted in the same way as mine, so that your telescope points slightly upwards while mine is truly level, you will decide that the climber started the ascent later than I did, and therefore that the climb to the top took less time. There is no paradox here, it is just that you took the start of the climb to be one point, while I took it to be another lower down.

Likewise with your example of the star. The Rocket takes the start of the stars movement to be a point in time 5 days ago, while the Earth observer takes it to be a point in time ten years ago. What the rocket takes to be the start of the trip and what the Earth observers takes to be the start of the trip are two separate events nearly ten years apart.

Answer 2

There is a star ten light years from earth, and at rest with respect to the earth. A rocket is passing the earth at 0.999999c. The clocks on the earth, star, and rocket all display "zero" at this time.

This is where the problem is. Since the rocket is moving with respect to the Earth and star, what is meant by "this time" depends on which reference frame you're talking about, as seen in the spacetime diagram below.

The red dashed line shows what it considered simultaneous in the Earth-star frame, while the blue line shows what is seen as simultaneous in the rocket frame. The reason why you calculated the time measured on the star to be less, when looking at the rocket frame is because you're starting the clock later, in that case. In other words, you're not measuring the same thing, thus causing the alleged "paradox."

---

In your edit, you said

In the rocket frame, the star takes just over 5.16 light days to reach the rocket (which regards its frame as being at rest), during which time the star clock changes by a negligible amount, due to time dilation being so great (gamma is 707) and the journey time in the rocket frame being so short (just over 5.16 light days).

This is incorrect. The time measured on the star clock is the proper time (a Lorentz invariant quantity) of the star's trajectory, which does not depend on reference frame. The proper time is given by $\tau^2=\Delta t^2-\left(\frac{\Delta x}{c}\right)^2$. Assuming that the star clock starts where the red $t=0$ line intersects with the star's worldline, then it will read a little over 10 years when the rocket reaches the star, regardless of the frame in which you calculate this.

Answer 3

Here is the picture you should have drawn (with the earth frame in black, the rocket frame in blue, and the star in red). (This is Sandejo's picture with a bit more detail.)

In the rocket frame, the trip takes .014142146 years, during which time the star clock advances by .00002 years.

Answer 4

In the earth frame the clocks on the earth, star, and rocket all display "zero" at this time.

Please note that in the rocket's frame the simultaneity is not the same as in the Earth frame. Hence, from rocket's perspective, at the time when it passes the Earth, the time on the star's clock is not "zero", but something about (10 years - 5.16 days).

In other words, the two events (a) clocks on Earth set to zero, and (b) clocks on star set to zero - are not simultaneous in the rocket's frame.

Answer 5

Here's a spacetime diagram in the spirit of @WillO and @Sandejo for the case of $(v/c)=3/5$ and $L=3$, first using light-clock diamonds (so we can calculate by counting) and then using hyperbolic-trigonometry (which can be generalized to your case of $(v/c)=(1-10^{-6})$ and $L=10$). See the associated Desmos url.

You seem to be interested in segments $XS$ and $XY$ and $XN$

"Think trigonometrically"... but rather than circular-trig functions, you'll use hyperbolic-ones.

---

$$v_{rocket}/c=\tanh\phi=\frac{OPP}{ADJ}=\frac{TS}{OT}=\frac{3}{5}$$ $$L=OX=TS=3$$ So, $$\fbox{$XS=OT=\frac{1}{(v/c)}TS =\frac{1}{(v/c)} L$} \qquad=\frac{5}{3}L =\frac{5}{3}(3)=5$$

Furthermore, $$\mbox{[time dilation factor]}\quad \gamma=\cosh\phi=\frac{ADJ}{HYP}=\frac{OT}{OS}=\frac{5}{4}$$

An important relation (Minkowski's version of Pythagorean theorem for a timelike hypotenuse): \begin{align} (ADJ)^2-(OPP)^2&=(HYP)^2\qquad &(5)^2-(3)^2=(4)^2\\ \\ (ADJ)^2-(ADJ \tanh\phi)^2&=(HYP)^2\\ \left(\frac{ADJ}{HYP}\right)^2-\left(\left(\frac{ADJ}{HYP}\right) \tanh\phi\right)^2&=(1)^2\\ \left(\cosh\phi\right)^2-\left(\cosh\phi \tanh\phi\right)^2&=(1)^2 \quad\longrightarrow\quad & \cosh\phi=\frac{1}{\sqrt{1-\tanh^2\phi}} \\ && \gamma=\frac{1}{\sqrt{1-(v/c)^2}} \end{align}

Note also that since $OS$ is Minkowski-perpendicular to $OY$,
then Minkowski-right-triangle $OXY$ is similar to triangle $OTS$.
So, $$\frac{XY}{OX}=\frac{TS}{OT}=v/c$$ and $$\frac{OX}{OY}=\frac{OT}{OS}=\gamma$$

Thus, $$\fbox{$XY=(v/c) OX= (v/c) L$} \qquad=\frac{3}{5}(3)=\frac{9}{5}=1.8$$ and [length-contraction] $$OY=\frac{1}{\gamma}OX=\frac{1}{\gamma}L \qquad=\frac{1}{\left(\frac{5}{4}\right)}3=\frac{12}{5}=2.4$$ Check (Minkowski's version of Pythagorean theorem for a spacelike hypotenuse):: \begin{align} (XY)^2 -(OX)^2 &=(OY)^2\\ \left(\frac{9}{5}\right)^2 -\left(\frac{15}{5}\right)^2 &=-\left(\frac{12}{5}\right)^2\\ \end{align}

Since $ON$ is a light-signal, then $\frac{c}{c}=\frac{OPP}{ADJ}=\frac{XN}{OX}$. Thus, $$\fbox{$XN=(1)OX=L$}.$$

---

The calculations are summarized in https://www.desmos.com/calculator/srlbwlgt79
I now invite you to modify $v/c$ to $0.999999 = (1- 10^{-6})$ and $L=10$. (If you use $0.999999$, then the Desmos-$v$ is a slider.)