1

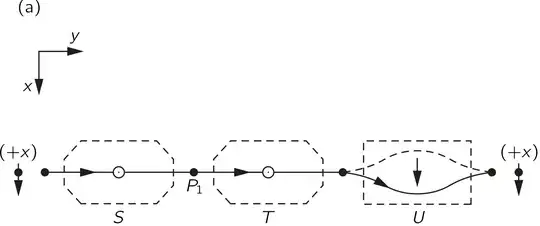
enter image description here

The figure above is taking from the Feynman lectures.Here $S$ ,$T$,$P_1$ and $U$ are Stern-Gerlach apparatuses.

$S$ and $T$ measures the spin in the $z$ direction where $z$ is pointing out of the page. The eigenstate associated with these operator are $z$ and $-z$.

$P_1$ is an apparatus that produces a state $+x$ and $U$ measures the spin in the $x$ direction so, its eigenstate is $+x$ and $-x$

As it is shown in the figure, Feynman is claiming that $U$ will measure always the state $+x$. I am not seeing why the state leaving $T$ is $+x$, since $T$ measures the spin in the $z$ direction ,so, the state leaving $z$ should be $-z$ or $+z$.

What I am misunderstanding here?

amilton moreira
  • 535

1 Answers1

1

A standard Stern-Gerlach experiment, as described in most QM textbooks, functions as follows:

Consider a particle system described by a Gaussian wavepacket moving in the x direction, which is in a superposition of spin.

\begin{equation} \lvert \Psi\rangle = \psi(x) \otimes (\lvert + \rangle + \lvert - \rangle ) \end{equation}

The system interacts with an external magnetic field aligned to deflect the particle either to the left or the right depending on the value of spin. This results in an entanglement between the spin part and the spacial part of the particles Hilbert space:

\begin{equation} \lvert \Psi\rangle = \psi_{left}(x) \otimes \lvert + \rangle + \psi_{right} (x) \otimes \lvert - \rangle \end{equation}

Detectors (LEFT and RIGHT) are placed to detect the presence of a particle in the left or right beam. So schematically the complete experiment can be described as

\begin{equation} \lvert \Psi\rangle \otimes \lvert {\rm LEFT~OFF} \rangle \otimes \lvert {\rm RIGHT~OFF} \rangle \to \lvert + \rangle \otimes \lvert{\rm LEFT~ON} \rangle + \lvert - \rangle \otimes \lvert {\rm RIGHT ~ON} \rangle \end{equation}

At this point you apply your favorite interpretation of quantum mechanics to justify that only one part of the sum on the rhs actually exists.

Consider instead a magnetic field tuned so that the left and right spacial wavefunctions end up back in a common central location before reaching a central detector. Then the entangled state could in principle be converted back into a disentangled state

$$\lvert \Psi\rangle = \psi_{center}(x) \otimes (\lvert + \rangle + \lvert - \rangle ) $$

So as far as future measurements are concerned, the magnetic field has not altered the spin state in any way. No measurement projection has occurred.

For analysis of the decoherence aspects of this setup please check this answer.

isometry
  • 2,110