Why does one experience a short pull in the wrong direction when a vehicle stops?

Question

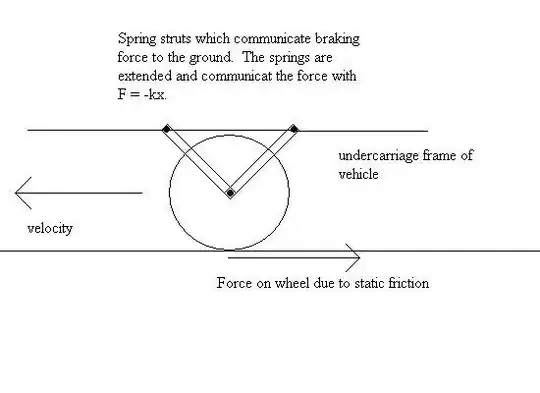
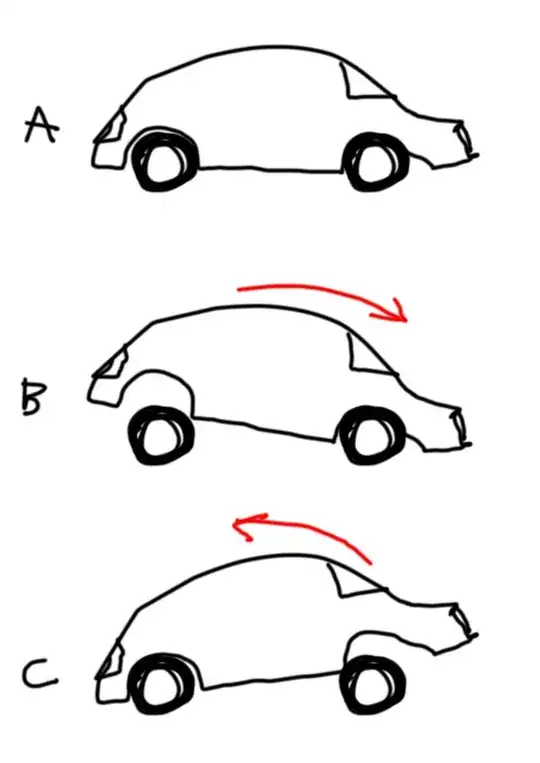
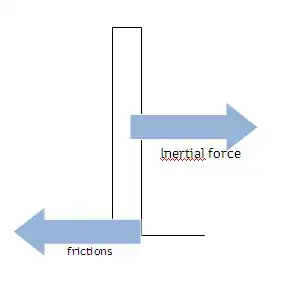
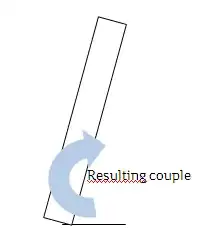
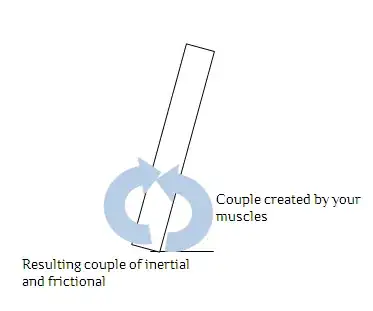
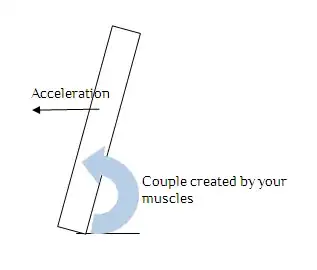
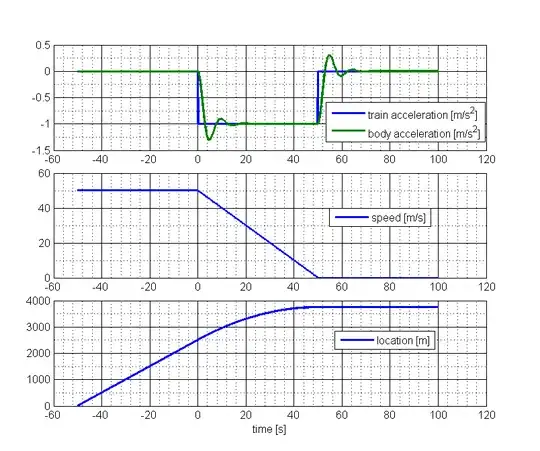
When you're in a train and it slows down, you experience the push forward from the deceleration which is no surprise since the force one experiences results from good old $F=m a$. However, the moment the train stops one is apparently pulled backwards. But is that a real physical effect or just the result from leaning backwards to compensate the deceleration and that force suddenly stopping?

---

So far the answers basically agree that there are two spring forces involved, for one thing oneself as already guessed by me and for the other the vehicle itself as first suggested in Robert's answer. Also, as Gerard suggested the release of the brakes and some other friction effects might play a role. So let's be more precise with the question:

Which effect dominates the wrong-pull-effect? And thus, who can reduce it most:

• the traveler
• the driver
• the vehicle designer?

---

edit Let's make this more interesting: I'm setting up a bounty of 50 100 (see edit below) for devising an experiment to explain this effect or at least prove my explanation right/wrong, and by the end of this month I'll award a second bounty of 200 150 for what I subjectively judge to be the best answer describing either:

• an accomplished experiment (some video or reproducibility should be included)
• a numerical simulation
• a rigorous theoretical description

update since I like both the suggestions of QH7 and Georg, I decided to put up a second bounty of 50 (thus reducing the second bounty to 150 however)

Answer 1

I spent last weekends making my own realisation of MPM method code (just for fun of it). I just had an idea that I can try to simulate something similar to the problem of interest.

So, here is our "car".

It is moving to the right with some constant speed. Then I apply some constant external force to the "wheels" to stop them. And that's what I've got:
1 2
3 4
5 6
The colours denote the amount of stress in the medium. And here is the animation:

Everyone are free to give other ideas for simulations/visualisations...

Answer 2

I drew up this picture below:

where upon returning to this page I see this question is 3 months old. However, I will answer this anyways, because nobody got the answer right in my opinion. The picture illustrates the springs or struts in the under carriage of the vehicle. In decelerating these communicate the deceleration from the road or rails to the vehicle. The deceleration is due to a static friction (holonomic or no slipping) between the tire and the ground, $F_b~=~-kx$. Here the braking friction is equal to the spring force the struts deliver. The braking force has a dependency on the velocity, where $F_b(v)~=~ F\theta(v)$, which is a heaviside function that turns off when the velocity equals zero. This means the spring has a slight distension when the vehicle comes to a rest and this then gives that little force forwards we experience.

It is often that people who do theoretical physics have never done things like rebuild a car engine.

Answer 3

I think several answers already pointed correctly to factors. But, at least in cars, I think the dominant factor is the set of front and rear springs. My illustration is very much exaggerated. In (a) we have a car with constant speed. When the driver gives the car a deceleration with the breaks the springs system enters in configuration (b). When the vehicle finally stops and there is no acceleration on it, the spring system oscillates back a little (c) before returning to the equilibrium configuration (a). The wrong pull effect happens between (b) and (c)

Answer 4

We have two effects going on. One is that the person is countering a constant acceleration, but when it rapidly stops there is nothing to stop the counterforce (lean) from creating acceleration of the person. The train is not a rigidbody, but in fact is a deformable body, so your intuition which assumes it posses infinite stiffness is wrong.. A deformable body under stress (to transmit the deceleration from the brakes to the distributed mass of the train car), is also under strain (i.e. the body of the train experiences some deformation). The instant the braking force is removed, these stresses and strains remain, and the train car is in a nonequlibrium state.

Try modeling it as mass on a spring attached to a rigid body. Subject the rigid body to a constant acceleration, and let the spring/mass come to its equilibrium position. Then eliminate the acceleration. The spring is not in its equilibrium position, and the mass will see acceleration.

Answer 5

There is no pulling, your body is pulling yourself because of the muscles' contraction to counter balance the deceleration.

Let's model your body by a mass reparteed vertically, plus a your feet. No force is applied, you are standing straight. Imagine we are at constant speed, the train driving from left to right on the picture.

When the vehicule decelerates, you are the subject of inertial force (if we consider the train as the reference, the inertial force aka fictious force greatly simplifies the explaination ; you could consider the earth as the reference and study the momentum instead).

Now let's consider you don't wear rollerblades. Your shoes have enough friction on the ground, and an opposite force is applied on your feet. The sum of these two forces is null, and you don't slide.

However, these two results in a couple) on your body, which begins to rotate.

Now, I'll assume you have a brain. Instinctively, the brain orders your muscles to contract to counteract this couple.

This muscular couple is created by your powerful calf contracting (i.e. pulling your body down), and your strong tibia has an opposite force.

All of sudden, the train stops, and the deceleration is null. What remains is your own couple. You pull yourself back.

Answer 6

I think @Robert's answer about 'up-whipping' might explain some of the effect in some cases, but I doubt it's noticeable in trains or other things with limited or no suspension travel.

I'm fairly certain it's mainly down to the 'leaning back' effect (the Kienzler effect??). Take a marble with you next time you travel by train, you can probably devise an experiment to find out!

Answer 7

You are pulled wrong way by your own hands and legs, which were stressed to keep you decelerating together with the vehicle.

When the vehicle suddenly stopped accelerating (this is how friction works: it is opposite to speed, and then speed suddenly reaches zero) then this tension keeps pulling you until you react and reconfigure.

Answer 8

A simple experiment:
Take a pendulum which is suspended using some support like a wooden frame.
Tape what happens when you stop.
Compare with video of you on the same train during the same stop.
Scientific enough and simple.
If the pendulum's motion differs from yours, your explanation is correct.

Sorry don't have numerical or theoretical explanation.

Answer 9

I think since the acceleration of the motion of the vehicle towards voyage direction is always <= zero for the slowing down process, the explanation has to be searched somewhere else since this cannot explain your "kickback".

To my opinion it might be that the slowing down acts on the vehicle also as angular acceleration such that it gets tilted a little (front "into the ground", back "into air"). At the point when the vehicle stops, this tilt will vanish (might be described by aperiodic oscillation). This movement, call it "up-whipping" will again have a turning point causing the kick into the seat.

Well, maybe :)

Answer 10

I believe this has to do with Jerk. Jerk is the derivative of acceleration. The brakes of the vehicle will provide a nearly constant force against the motion of the car. Since $F=m a$, as your vehicle slows at a constant rate of negative acceleration. Once the car stops, the force (and consequently your acceleration) go to zero very quickly. This results in a high amount of Jerk, and this is what you're feeling.

Answer 11

Although I'm really late to the game, I would like to chime in by saying that in the course of implementing automatic-guided-vehicle control systems (wire-guided vehicles with set courses), I've had occasion to ride vehicles while experimenting with their acceleration and deceleration curves; one thing I've notices it that the human body (well, mine in particular, but I assume others are similar) is remarkably sensitive to changes in acceleration. If the vehicle's speed is slowed linearly to zero, the deceleration will feel smooth until the speed reaches zero, whereupon almost no matter how slow the deceleration, or how slowly the vehicle was traveling when it stopped, the change of deceleration from non-zero to non-zero will be perceptible. Spreading out the change of deceleration over 1/10 second may not visibly affect the motion of the machine at all (if a machine is decelerates uniformly at 10mm/sec/sec it's only going to travel 0.05mm in its last 100ms; smoothing out the deceleration curve won't add even 0.05mm to the total travel distance) but can have a noticeable effect on how the ride feels.

Answer 12

I think this effect is caused by the overshooting in the response of the body to the change in the train's acceleration.

Suppose there is a "perfect" train that can start/stop acceleration (breaking) instantaneously. It starts slowing from speed 50 m/s and until it reaches the zero speed.

Here is a simulation. The "body" model is very approximate, but demonstrates the effect. As we know, we experience similar effect when train begins slowing.

I took the moving "body" model from here: http://en.wikipedia.org/wiki/State_space_representation#Moving_object_example

Answer 13

Bit late to the game, but if we put a glass of water on the train in these circumstances you will see the water pushed to the "front" side of the glass as the train slows and then, when the train comes to a stop, swish to the "back" side of the glass, repeating in broadly diminishing cycles until coming to a rest.

The human body is certainly more rigid than a water in a glass, but your organs (and brain which is pretty heavy) will follow the waters pattern of motion and kick back.

Now try the same thought experiment with a glass of frozen solid water. No kickback.

I guess the answer is fluid dynamics combined with deceleration.

Answer 14

Another way of observing this effect is to have a car go up a gentle slope at some speed, put it in neutral gear, wait for it to stop and then hitting the breaks. Most people expect that using the breaks when the car is at rest (even if just momentarily) will have no perceptible effect, and they are surprised to feel a 'jerk' very similar to the one mentioned in the question.

Answer 15

The explanation comes from standard mechanics where a body is in equilibrium when the forces acting on, and torques about the centre of mass sum to zero.

When the train is decelerating, there are torques acting on your body where it makes contact with the train via the seat or floor, and you automatically alter your body postition to create counter-torques so that your body remains in equilibrium. When the train suddenly stops, this net counter torque is no longer balanced, and so you rotate about your centre of mass in a direction that pulls you back.

Answer 16

And thus, who can reduce it most: the vehicle designer !

The French car maker Citroen do the compensation since long time ago.

quoting from citroenet

Anti dive suspension is incorporated since the rear brakes take their fluid from the rear suspension which pulls the tail down under heavy braking.

Answer 17

Perhaps it can be explained like this:
At a certain moment the train pilot releases the brake system. At that point the heavy mass of the train is released from a rather powerfull constraint and it's wheels can move freely (well not completely free of course). When the wheels turn slightly forwards you experience a force in the other direction. The mass of the train being quite large and the release of the brakes quite sudden, this force is stronger then the previous carefull deceleration.

So the short pull wouldn't be in a "wrong" direction.
I should be easy to verify in reality whether this explanation is correct.