Flat Earth interpretation of Newtonian gravity

Question

Consider a projectile body launched from the earth's surface with a speed lower than the escape velocity.

The orbit of the body under Newtonian gravity traces an ellipse which intersects with the earth's surface, resulting in a collision. However, if we approximate the motion as a simple projectile instead, using the flat earth assumption (with position invariant vertical gravitational field), then the trajectory recovered is a parabola. Please see this physics.se post and answers therein for a detailed discussion of why the trajectory is a parabola.

From the above analysis, can we conclude that a segment of an ellipse represented in the local coordinates (say with origin at one end of the segment and a coordinate axis along the segment) a parabola?

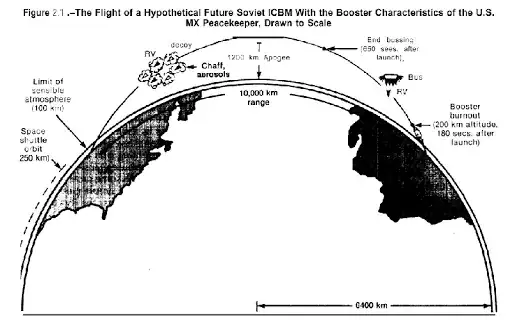
Note: The referenced parabola is not limited to the curve trajectory traced by the projectile from start to end point but also includes all segments along the elliptic trajectory. For instance, in the figure below, the ellipse segment from the 'booster burnout, 180 seconds after launch' point to 'end bussing, 650 seconds' point can be approximated as a parabola by considering constant gravity equal to, say, the average gravity over the elliptical trajectory.

Answer 1

If you zoom in close enough on any continuous curve such that $(t-t_{0})^3 \approx 0$, then, the curve will be indistinguishable from a parabola. And since you can taylor expand around any point, you can do this anywhere.

This is basically just rediscovering Runge-Kutta integration, where you pick some step size $\Delta t$, and an initial value for $x$ and $\dot x$ (add y and z if you want, the procedure is the same, with more dimensions). Then, at each timestep,

1. compute $F(x)$ using whatever force law you're integrating (in your case, $F = mg\left(\frac{R^2}{r^{2}}\right)$, where $R$ is the radius of the earth, and $g$ is the acceleration due to gravity at the surface)
2. evaluate the position and velocity at the next timestep:
1. ${\dot x}_{t+1} = {\dot x}_{t} + \frac{F\Delta t}{m}$
2. $x_{t+1} = \frac{1}{2}\frac{F}{m}\left(\Delta t\right)^{2} + {\dot x}_{t}\Delta t + x_{t}$
3. repeat until evolved for the desired amount of time, if accuracy is bad, make $\Delta t$ smaller

Which is precisely pretend the motion is a bunch of parabolas, and just recalculate the forces at every point. This is, in fact, the easiest way to make a semi-reasonable 3-body problem numeric solver in Newtonian gravity.

Answer 2

The ellipse and the parabola are tangent to each other at the launch site, and their curvatures (determined by local acceleration at the launch site, which is the same for "flat earth" and "spherical earth" by definition) are locally the same. Further away from the launch site, they will diverge.