What exactly is the physical quantity referred to as 'wave-front' in Huygens's principle?

Question

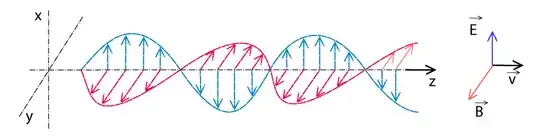
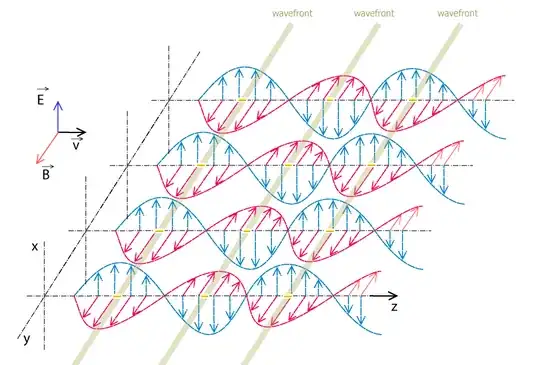
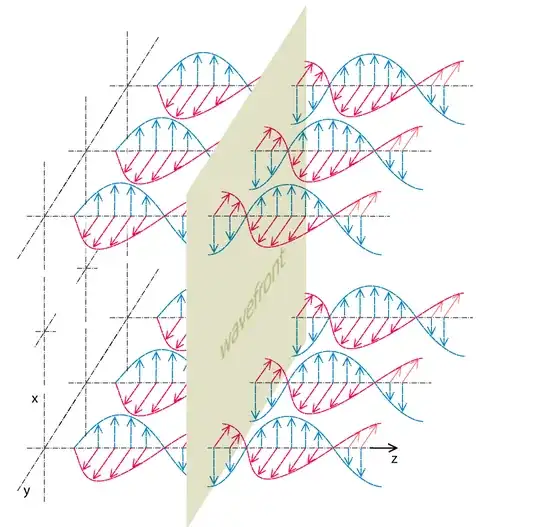
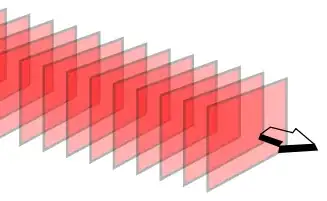
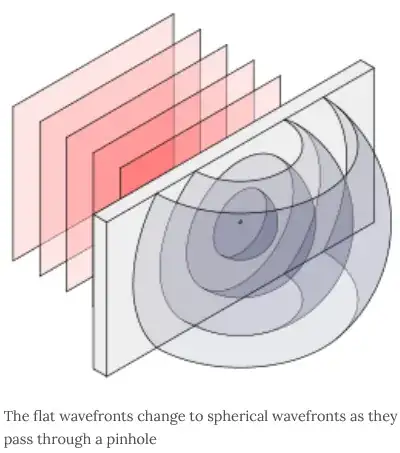
Huygens’s principle states that every point on a wave front is a source of wavelets that spread out in the forward direction at the same speed as the wave itself. The new wave front is tangent to all of the wavelets. From

I'm having a hard time understanding what a 'wave front' means for a spherical wave. I can understand it for transverse waves as the peaks of it but how do we have a 'notion' of peak for a spherical wave?

Secondly 'oscillations' of what is involved in classifying wave front? I've read this answer that Huygens's is about propagation and not emission but I can't understand what exactly is being propagated. Would it be correct to think that it's photons?

Clarification on the classifying point: In sound waves we say that it is density of the air which we use to classify wave fronts but what exactly is the physical quantity in classifying wave fronts for electromagnetic waves?

Answer 1

I'm not entirely sure where your confusion lies, but I have a feeling that it's of a conceptual nature, so maybe this will help clear things out a bit. Here's a one-dimensional EM wave; it's a wave of changing strengths of the electric and the magnetic fields.

The wave propagates from left to right, along the positive z-axis. Again, this is the one-dimensional case; the electric and the magnetic field permeate the z-axis. In other words, every point along the z-axis has two vectors associated with it, and these vectors have a magnitude - that is the physical quantity that oscillates. The vectors form form a wave pattern.

---

Let's move one dimension up; now, the electric and the magnetic field permeate the yz-plane:

For every point on the yz-plane there's a $\vec E$ and a $\vec B$ associated with it; their magnitudes change in a wave-like pattern, forming a 2D version of a plane wave of light. The wavefronts are simply lines that connect points that are in phase. Note that there's (continuously) infinitely many wavefronts, the image just shows a few representative ones.

---

Here's the 3D case; now the electric and the magnetic field permeate all of space:

The wavefront is now a plane that connects points that are in phase. As before, this is a plane wave, with parallel wavefronts moving from left to right along the positive z-axis.

(image from Wikipedia)

---

For a spherical or a hemispherical wave, the idea is exactly the same; it's just that the wavefronts are curved segments of a sphere:

(image from here)

Answer 2

Perhaps a sound wave is a good way to start.

What is 'oscillating' at each point is the air pressure. If someone made a loud 'clap' sound, the region of sudden high/low pressure would travel outward and the places it had reached at a given time would be in the shape of the surface of a sphere.

The air itself is not moving outward from the centre, the air on the whole is more or less stationery, just the pressure wave moves outwards and the wave-front is the surface of the sphere.

If you imagined every point on the sphere starting new wavelets, a short time later the influence of the wave from all those points would have reached the surface of a new sphere with slightly larger radius.

For light it would be similar, but it's the strength of the electro-magnetic field that varies.

Answer 3

It seems that you are looking for a way to precisely locate a point on a wave where you can say, "the phase here is pi/4", or "the amplitude here is maximum", and conclude that the wavefront passes through that point. Unfortunately, it's not that clear-cut. To really measure phase, multiple waves in a train must be observed because phase is a relative quantity. Phase is not absolute.

When there are two sinusoidal wave trains, identical except for their direction, crossing at a point, it's not too difficult to define and measure a phase difference between them at that point. All you need to do is delay one of the wave trains just enough so that the two waves are perfectly synchronized; then you compare that delay to the period of the wave train. If the two wave trains aren't sinusoidal but are still identical and periodic, then you compare the delay to the fundamental period of the wave trains.

An isolated wave front doesn't really have a period. It therefore also doesn't really have a phase. When we apply Huygens Principle, we generally take it as given that the wave train is continuous, uniform, and sinusoidal. In that case, any constant-amplitude surface at a given instant can be taken as having phase "zero" or "$\pi/2$, or whatever; and the Principle works.

All that said, neither absolute phase nor absolute amplitude are well-defined for an arbitrarily-shaped wave. In the general case, anything you decide to call "absolute phase" or "absolute amplitude" is going to be constantly changing; and amplitude will not correspond directly to phase.

Answer 4

In physics, the wavefront of a time-varying field is the set of all points where the wave has the same phase of the sinusoid. The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency. Wavefronts usually move with time. Wikipedia

However, I think it can also be defined for non sinusoidal waves as the leading edge of the wave. For example, if the 1D, 2D, or 3D propagating wave was a step function the wavefront would be the location of the step.

Also I think it can be defined as the tangential surface to all of the Huygens' wavelets: https://www.dictionary.com/browse/huygens-principle

Huygens principle the principle that all points on a wave front of light are sources of secondary waves and that surfaces tangential to these waves define the position of the wave front at any point in time.