1

In the Standard Model of QM, all forces are mediated or carried by particles (for want of a better word) called bosons. The photon is an example of a force-carrying gauge boson, and mediates the electromagnetic force.

The electrostatic and magnetostatic forces are not mediated by real photons, and the answer here explains that they are not mediated by virtual photons either, while the answer here goes way over my head.

Put simply, what particles are these forces carried by - or aren't they after all?

As an example, consider a charged fragment of paper levitated above a charged metal plate. Nothing appears to be moving or changing its momentum or anything; no work is being done, no energy is going anywhere. The electrostatic levitating force is counterbalanced not by another electromagnetic force but by gravity. How does that work, then?

Guy Inchbald
  • 7,578

2 Answers2

3

I have never liked the "virtual particles" concept; they're the result of taking Feynman diagrams a tad bit too literally. Feynman diagrams are nice little pictorial representations of terms in a perturbation series designed to calculate scattering elements between two particles; there's one in anna v's answer. However, these should not be taken as literal pictures of what is going on.

Scattering in quantum mechanics is due to interactions between fields. Two particles (which are derivative from a field, see this answer) in approximate momentum states interact for some finite time and then asymptotically go to some other particle states in the far future (where interactions become negligible). This process is encoded in the LSZ reduction formula, and is our current understanding of how things go about; fields interact with each other. For example, the electron field might interact with the photon field, and this produces scattering.

In the non-relativistic limit, when scattering is not very large, we can neglect all but the leading order term in the perturbation series (encoded in the diagram in anna v's answer). Now, because we are in the non-relativistic limit, we can assume the Bohr approximation from regular QM holds. Thus, we can pretend the scattering is actually due to some potential, which comes out to be the Coulomb potential. However, in the end, it is (to the best of our knowledge) just fields interacting with other fields.

John Dumancic
  • 4,077
0

At the quantum framework, everything in the world is made up by the particles in the standard model of particle physics and their interactions. All other theories can be shown mathematically to be emergent from this level.

The macroscopic electric and magnetic fields are the result of the addition of a high number of charged quantum particles, what is a "force" at the quantum level is built up to "force" of classical level electric and magnetic fields.

What is the electric "force" at the quantum level? It is the exchange of dp/dt, (p a momentum vector) between two interacting charged particles, for example two electrons, a first order term in the expansion in series for the solution :

e-e-

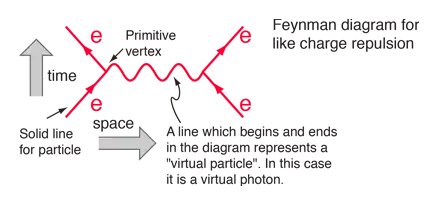
The diagram is a recipe for writing the integrals necessary for a calculation of the probability of interaction between two electrons.

The dp/dt is assigned to the virtual photon connecting the two vertices. Virtual particles are a mnemonic to help in conserving the quantum numbers characterising the interaction.

In principle, no matter how far away are two electrons , they will be interacting with such a virtual photon. In order to detect an electric field there must be an interaction at the quantum level. When distances are large, the classical "force" can be defined within classical electrodynamics.

So in a nonmathematical description one can say that a static field is built up by virtual photons. A test charge measuring classically the static electric field reacts with F=ma , and F is the sum of the dp/dt for each individual quantum interaction . Considering that the number of fundamental charges are of the order of ~ $10^{23}$ (avogadro number) it is better to use classical electrodynamics.

anna v
  • 236,935