2

I am trying to combine the spin of two particles.

Their individual spins are:

$|1,0\rangle $ and $\left|\frac{1}{2},\frac{1}{2} \right>$

Now I am told that they combine to give a total spin state of:

$$\left|\frac{1}{2},\frac{1}{2} \right>$$

However, I am confused as to how this works. Thinking physically I am confused as:

an image showing how the first state has a magnitude of one, just not in the measurement direction (z), and the second has a magnitude of 1/2 but in the z-direction. Hence combining the two gives a measured value of 1/2 in the z-direction, however, I am confused as to how the total vector has a magnitude of 1/2? combining the perpendicular vectors would suggest a magnitude of sqrt(5)/2.

I understand that this doesn't really make sense as spin is quantized, however, I am confused as to how the states combine if this is not the case.

Himanshu
  • 12,211
helpwithphysics
  • 53

2 Answers2

3

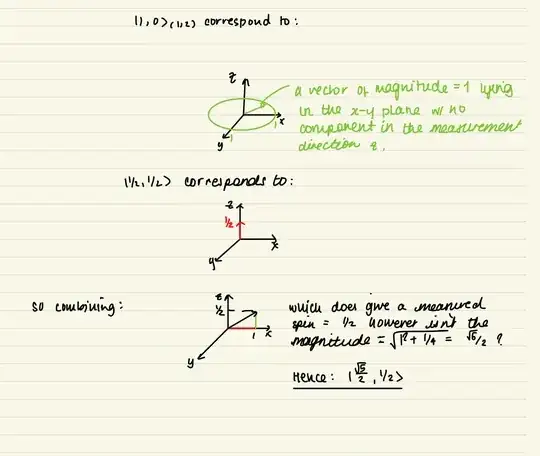
$ \newcommand{\ket}[1]{{\textstyle\left|{#1}\right>}} \newcommand{\sqrtfrac}[2]{{\color{lightblue}{\textstyle\sqrt{\frac{#1}{#2}}}}} %%% $There is no way to combine $\ket{1,0}$ and $\ket{\frac12, \frac12}$ to get a pure $j=\frac12$ state. The only possible value for the $z$-axis projection $m$ is $0 + \frac12 = \frac12$, but the total angular momentum can take either of $\frac12$ or $\frac32$.

The orthonormal combinations are given by the Clebsch-Gordan coefficients, which are usually presented in horrible tables like

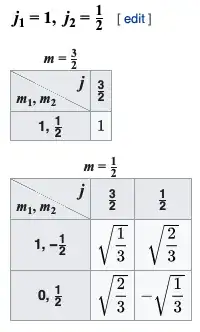
wikipedia screenshot

The way to read this horrible table is that, if you wanted to construct the composite state like $\ket{\frac32,\frac12}$ or $\ket{\frac12,\frac12}$, you would read down the columns of the second table:

\begin{align} \ket{\frac32,\frac12} &= \sqrtfrac13\ \ket{1,1}\ket{\frac12,{-\frac12}} + \sqrtfrac23\ \ket{1,0}\ket{\frac12,{+\frac12}} \\ \ket{\frac12,\frac12} &= \sqrtfrac23\ \ket{1,1}\ket{\frac12,{-\frac12}} - \sqrtfrac13\ \ket{1,0}\ket{\frac12,{+\frac12}} \end{align}

If your constituent particles are in a pure state $\ket{1,0}\ket{\frac12,\frac12}$, your composite system is in a superposition of $\ket{\frac12,\frac12}$ and $\ket{\frac32,\frac12}$. You should convince yourself that you can find its coefficients either by solving the system of equations above for $\ket{1,0}\ket{\frac12, \frac12}$, or by reading across the Clebsch-Gordan table.

Photon
  • 5,067
rob
  • 96,301
0

This can be done as follows: $$1\otimes \frac{1}{2}=\frac{3}{2}\oplus\frac{1}{2}$$ Using the notation $|j_1m_1,j_2m_2\rangle $ for product ket and $|jm\rangle$ for sum ket.

$$|j_1m_1,j_2m_2\rangle =\sum_{j,m}|jm\rangle \langle jm|j_1m_1,j_2m_2\rangle $$ $$\left|10,\frac{1}{2}\frac{1}{2}\right\rangle=\left\langle \frac{1}{2}\frac{1}{2}\left|10,\frac{1}{2}\frac{1}{2}\right.\right\rangle \left|\frac{1}{2}\frac{1}{2}\right\rangle+ \left\langle \frac{3}{2}\frac{1}{2}\left|10,\frac{1}{2}\frac{1}{2}\right.\right\rangle \left|\frac{3}{2}\frac{1}{2}\right\rangle$$ Putting the value of Clebsch-Gordan coefficient from here.

$$\left|10,\frac{1}{2}\frac{1}{2}\right\rangle=\sqrt{\frac{2}{3}}\left|\frac{3}{2}\frac{1}{2}\right\rangle-\sqrt{\frac{1}{3}}\left|\frac{1}{2}\frac{1}{2}\right\rangle$$

Himanshu
  • 12,211