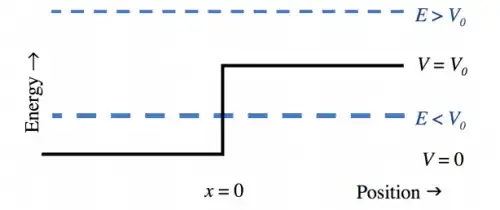
When an electron with E < V approaches a step in potential energy, the wave function will exponentially decay at the step, meaning there is still a finite possibility of the electron being found at x > 0:
My question: presumably the electron can't be found "inside" the step? So if it is found at X > 0, would it be found with E > V (i.e. above the step)? Or does such tunneling only have a meaning if the decaying wavefunction can reach the other side of the step?
If the energy of the electron $E<V_0$, then the wave function of the particle will be exponentially decaying for $x>0$. The wave function to the right of the step is exponentially decaying over a distance of $1 /(k_2)$.
The energy of the particle can be found as $$\langle \psi|H|\psi\rangle=\langle \psi|\frac{P^2}{2m}+V(x)|\psi\rangle =\frac{1}{2m}\langle \psi|P^2|\psi \rangle +\langle \psi|V(x)|\psi\rangle $$ Put the wavefunction, and find the expectation value for the energy.
