UPDATE: Since the OP updated the question, I have updated this answer (see below).
UPDATE2: In order to further address the comments of the OP, I have added two more spacetime diagrams.
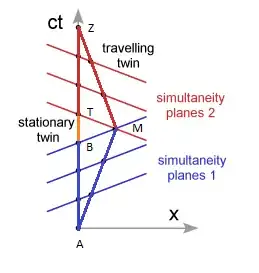
It might be helpful to visualize the spacetime-diagram of the light-clocks involved in the Clock Effect.
It provides a mechanism that can be used to operationally define how time is measured.
On rotated graph paper, it can be seen that the "light-clock diamonds" (the causal diamond between consecutive ticks of an inertial clock) have the same area [as required by lorentz invariance (since det L=1)].
Below are clocks for inertial observers RED, BLUE, and GREEN.
BLUE has velocity 0.8c(= (4/5)c ) with respect to RED, and
GREEN has velocity of -0.8c(= (-4/5)c ) with respect to RED.
These inertial light-clocks measure the proper time along these inertial paths.
- Of course, the "traveler" who left RED and later reunites with RED
undergoes acceleration since she must use a non-inertial path BLUE-THEN-GREEN (which is piecewise-inertial, but nevertheless non-inertial).
- One can imagine the "traveler" releasing the BLUE clock and grabbing onto [or merely traveling along with] the GREEN clock, or merely using the clocks along those inertial worldlines. These clocks are inertial.
- One can also imagine the "traveler" carrying her own clock along the piecewise-inertial worldline, which must match the intervals with the corresponding inertial clock alongside on that inertial portion of the trip.(*) In this case, the "traveler"-clock also undergoes acceleration.
- (*) From Geroch's General Relativity from A to B, p. 80:
The upshot of our property of clocks is this. Given any world-
line of a particle, one acquires an assignment of times to points
of that world-line. (Physically, the assignment is obtained by
carrying a clock alongside the particle, and using the readings
of the clock to obtain the "times.") This assignment of "times"
to the points of the world-line of any particle is unique as far as
time differences are concerned. (Here is where we are using our
property of clocks. When we say "carry a clock alongside the
particle" we do not specify the past history of the clock. We
are thus assuming implicitly that ticking rates are independent
of past history.) To summarize, world-lines of particles now
acquire time-functions.
UPDATED
https://www.desmos.com/calculator/8kr9uc9zwu
(v.9e of my spacetime diagrammer [for the Twin Paradox / Clock Effect] )
Update
To answer your questions, you can read off information from my diagram.
This approach is a "visualization of proper time"
by visualizing the spacetime-diagram of a light-clock,.
My interactive Desmos application has some features that can be turned on:
"simultaneity" and "time dilation" and "doppler".
"Simultaneity" is identified by the spacelike diagonal of the observer diamonds.
I'll address your added questions below this diagram.
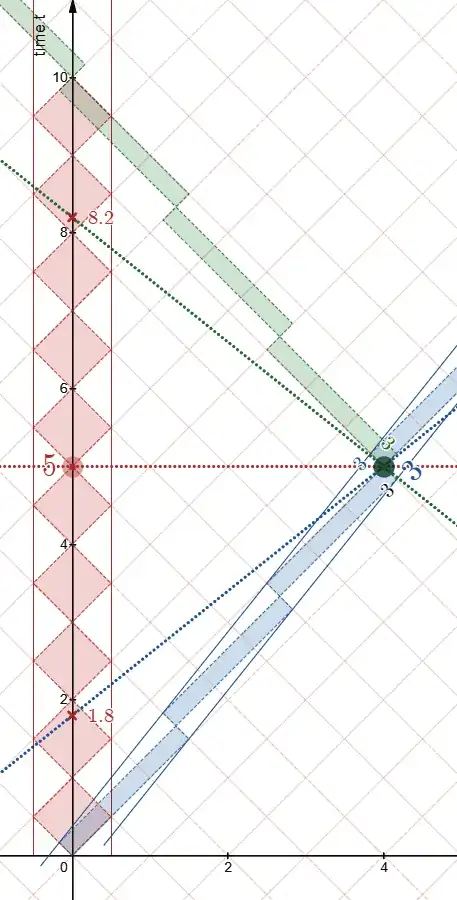
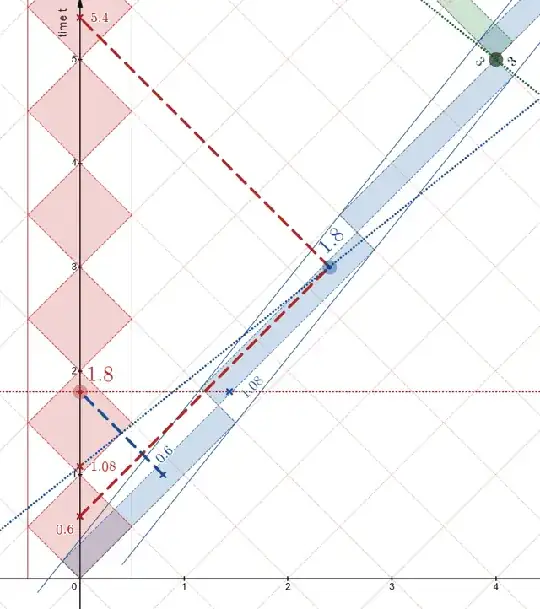
Note that the traveler in the diagram has, by counting diamonds,
speed = (4/5)c = 0.8c, there and back.
the time-dilation factor $\gamma =\ 5/3 $.
Hence, (5)=(5/3)(3) along RED's simultaneity (your "S")
and (3)=(5/3)(9/5)=(5/3)(1.8) along BLUE's simultaneity (your "outbound O").
--Refer to the diagram above.--
Doppler factor $k=3$, which is associated with the stretching of the diamonds, by a factor 3 in forward direction and by 1/3 in the other direction.
Follow the worldlines of light-rays along the light-cones.

There is an important subtlety involving such "videos":
one needs to distinguish
- "simultaneity of distant events" (the "assignment of t-coordinates" done by each observer using radar-measurements or a line of distant clocks associated with the observer) following the lines parallel to the clock's spacelike diamond-diagonals. This involves "time-dilation". This is essentially "map making".
- "visual appearance" (the "seeing" done by each observer using light-signals that are received on that observer's worldline) following lines along the light-cones (along 45-degree lines, the diamond-edges). This involves the "Doppler effect". This is essentially "viewing a movie [of light-rays striking your eye or film]".
Onward to your questions...
- Will the S video section AB align O video section AM ?
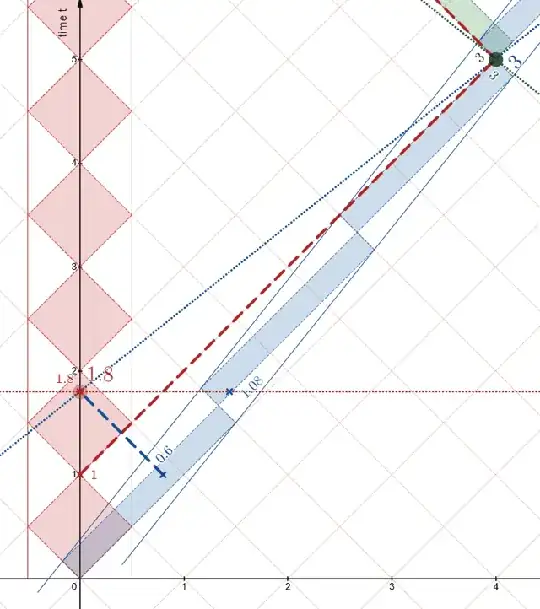
NO.
According to S
event B (on S @ 1.8) occurs at t=1.8 according to S
event M (on O @ 3) occurs at t=5 according to S (see the first diagram)
If S makes an animated chart (an animated spacetime diagram) that develops as S's clock evolves, when B appears at t=1.8, the event Bsim (on O @ 1.08) on O's worldline appears. S assigns both events t=1.8 and says that B and Bsim are simultaneous. (Why 1.08? That's 1.8/(5/3), from Time Dilation. Think similar triangles, comparing with first diagram.)
If S makes a movie with a camera (receiving light from outbound observer O),
when B appears at t=1.8, the light-flash-signal from the event Bpas (on O @ 0.6 ) appears in the movie. Imagine that each clock emits the light on its display telling the time.
All S can say is that when S's clock reads (at B) 1.8, S received light from O with the reading of 0.6. (Why 0.6? That's 1.8/(3), from Doppler.)
According to O
event B (on S @ 1.8) occurs at t=3 according to O
event M (on O @ 3) occurs at t=3 according to O
If O makes an animated chart (an animated spacetime diagram) that develops as O's clock evolves, when B appears at t=3, the event M (on O @ 3) on O's worldline appears. S assigns both events t=3 and says that B and M are simultaneous.
If O makes a movie with a camera (receiving light from observer S),
when B appears at t=3, the light-flash-signal from event B (on S @ 1.8 ) appears in the movie. Imagine that each clock emits the light on its display telling the time.
All O can say is that when O's clock reads (at M) 3, O received light from S with the reading of 1.8.
What would O say when O's clock reads 1.8?
O obtains the same results when O's clock reads 1.8
that S obtained when S's clock reads 1.8
...in accordance with the principle of relativity since O and S have been inertial observers since their separation event.
I think this gives you enough of a headstart
(and an interactive tool) to answer the rest of your questions.
UPDATE 2
My Desmos application has a "boost" feature to view the situation
from different frames. (In this version, the rotated graph paper grid
for the incoming leg hasn't been drawn.)
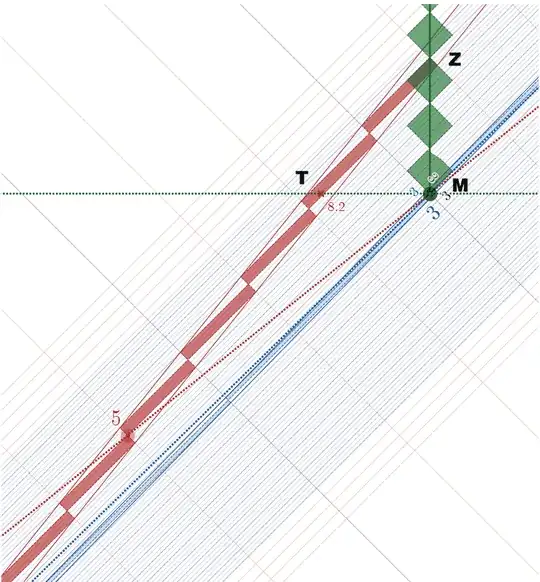
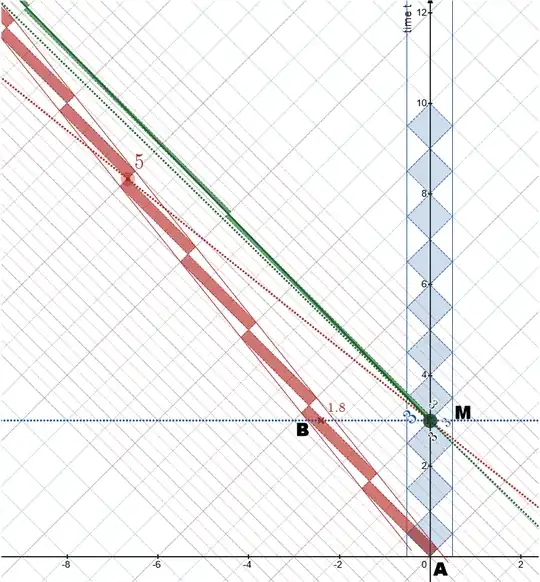
Here is the incoming leg, followed by the outgoing leg
in the same spirit of my answer to another question (linked at the end)
to attempt to construct a spacetime diagram for a non-inertial observer.
Stitching together the diagrams for outgoing (AM) and incoming (MZ) legs
leads to a single diagram which is not a real spacetime diagram because of some peculiar features discussed in that earlier answer (linked below).
For example, the inertial observer (AZ) has a discontinuous worldline in this diagram (jumps in t-assignments, irregular clock-readings, and jump in position [when the incoming leg has a different speed from the outgoing leg]).
This Frankensteined diagram is clearly not equivalent to the spacetime diagram of the inertial traveler from A to Z.
By following light-rays along the light-cones (along the diamond-edges), one can track
the transmission and receptions of the "clock-face images",
if one want to understand what each traveler "sees" or "captures on film".
For more details [including a reference to my paper], and for a discussion of how the non-inertial "traveler"
is not equivalent to the inertial stay-at-home RED observer,
visit my answer
https://physics.stackexchange.com/a/507592/148184
for this question
What is the proper way to explain the twin paradox? .