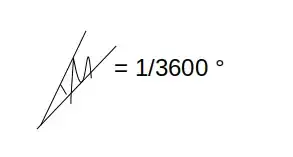How does a proper motion displacement of $x$ arcseconds/year mean a star is moving at $x$ AU/year?

Question

I trying to understand the author's answer to this question:

I don't understand the part underlined red. How does 3.6pc mean 3.6AU? It says a "distance of 3.6AU", but doesn't say what is being measured to or from. So until I understand this, that calculation of $v_{\perp}$ makes no-sense to me.

After searching the internet and then this exchange site, I stumbled upon this question which is pretty much asking the same thing I am in this question. I don't understand part of one of the answers given to this post by @Profrob:

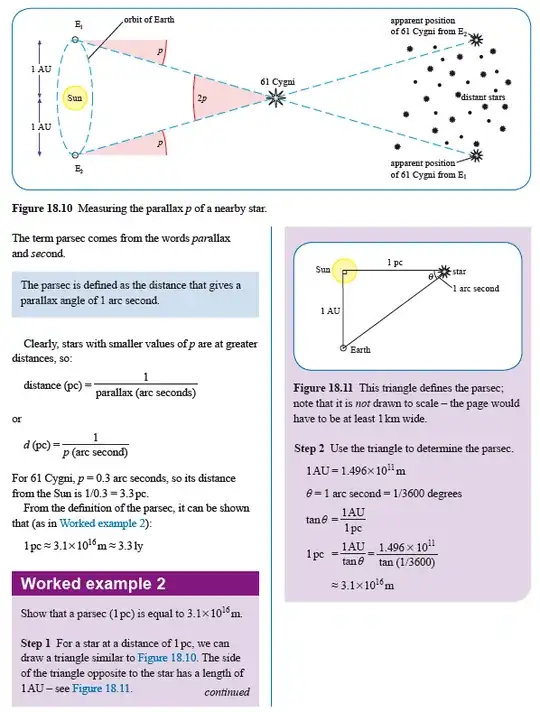
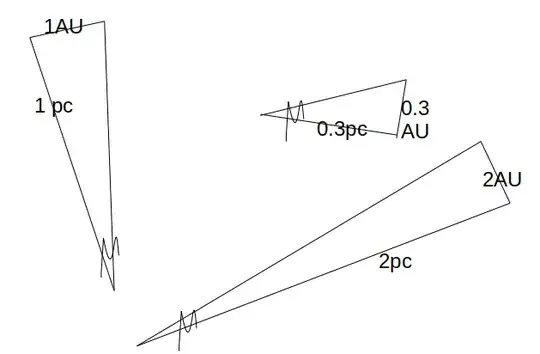
The definition of Parallax is that the 1 AU radius of the Earth's orbit around the Sun causes an angular change of 1 arcsecond in the apparent position of a star that is 1 parsec distant. But this definition can be extended to any angular displacement. Thus if a star is 1 pc away, a proper motion displacement of $x$ arcseconds/year means it is moving at $x$ AU/year. If it is at a different distance we just scale up by the distance in parsecs.

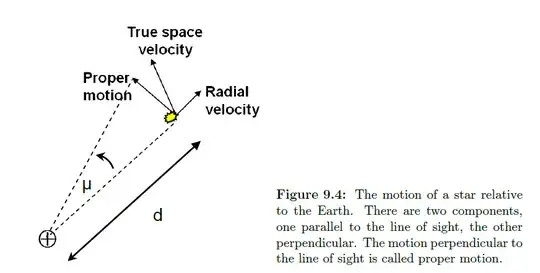
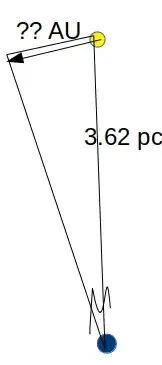
In the diagram above (which I borrowed from the question I linked) the Earth is facing along the line of sight towards a star that is moving perpendicular to the line of sight with transverse velocity, $v_{\perp}$. The problem however is that in the answer given by @Profrob he mentions that "a proper motion displacement of $x$ arcseconds/year means it is moving at $x$ AU/year" but according to page 268 of this textbook (Physics 2) by OCR published by Cambridge University Press:

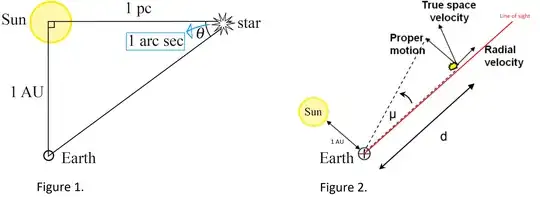
In the image within the worked-example 2 box, the parsec is being measured from the Sun to the star, not from the Earth to the star which is the case for the proper motion diagram at the start of this question. That is the first problem, the second problem is that the proper motion, $\mu$, in the proper motion diagram at the start of this question is being measured from the LOS (line of sight, in red below) of the Earth connecting the moving star (with line segment $d$ (pc) in arcsec), I have made two figures below to illustrate my confusion:

In figure 1, the situation is fine as the mean Earth-Sun distance is opposite the angle of interest, $\theta$, of 1 arcsec. But the Sun is nowhere near the moving star with proper motion $\mu$, last time I checked it's next to the Earth (which is why I placed it next to the Earth in figure 2.)! So how can 'a proper motion displacement of $x$ arcseconds/year mean the star is moving $x$ AU/year'?

So to wrap this up why is $$v_{\perp}=\frac{4.71\cdot 3.6\cdot 1.5\times 10^{11}\mathrm{m}}{3.15\times 10^7\mathrm{s}}=80.7\,\mathrm{km}\,\mathrm{s^{-1}}?$$

---

P.S. Apologies if I don't respond straight away to potential comments and/or answers as it took ages just to write this post and now too tired so need sleep, goodnight.

Answer 1

Whether you measure distance from the Earth or the Sun is of little importance, since even the nearest star is about $3\times 10^5$ further away than the Earth is from the Sun. Thus the lengths of the long sides of any triangle you draw involving the Sun, the Earth and the distant star are practically the same.

The distance to the star is defined as the triangle side between the Sun and the star though.

You have twice selectively quoted my previous answer. It isn't true that "a proper motion displacement of x arcseconds/year mean the star is moving x AU/year", but it is true that "if a star is 1 pc away, a proper motion displacement of x arcseconds/year means it is moving at x AU/year".

If a star changes its angular position by x arcseconds and it is 1 pc away, then it has moved by x au (in the plane of the sky). This can be seen by drawing a simple triangle between the two stellar positions and the Sun (or the Earth, since to better than 1 part in $10^5$, the lines from the Earth to the two stellar positions will also have an angle between them of 1 arcsecond). The measurement of this change in angular position is quite separate to measuring a parallax, which is the semi-amplitude of the annual oscillation in apparent position as seen from the Earth, and is what defines a parsec in terms of an annual parallax of one second and the au.

If the star moves by x arcseconds and it is 2pc away, then it has moved by 2x au (by similar triangles).

etc.

Answer 2

Both diagrams are correct. They show the relationship/definition that a transverse length of 1AU at a distance of 1pc subtends an angle of 1 arcsecond. In the first example, the distance is the Sun-Earth distance of 1AU, as `seen from' the Star. In the second diagram the distance is the (apparent) length travelled by the star, as seen from the Earth. (Ignore the sun in the second diagram - it is there to indicate how 1AU is originally defined). You can draw such a right triangle with an angle of 1arcsecond between any 3 points in space with the required distances of 1AU, 1pc and get an equally valid example to illustrate their definitions.

The second diagram is the more useful way to think about it to solve the initial question. When d=1pc, as in the linked question, then by definition an angle of 1 arcsecond corresponds to an opposite side of 1AU. In your question, however, the distance d=3.62pc, the angle $\mu$ is the same 1arcsecond, and the distance $x_T$, opposite the angle, is unknown.
At this point it might be obvious to you, by intuition about the intercept theorem, that the distance $x_T$ must also be scaled up by $\times 3.62$ from the original $1AU, 1pc$ situation. If not we can show the math:

Relating the definition (shown in Figure two) $$\tan(\mu) = const = \frac{1AU}{1pc}$$ and the situation in your question $$\tan(\mu) = const = \frac{x_T}{3.62 pc}$$ where we don't have to know what $\tan(\mu)$ is, but it is the same value in both cases. Putting them together: $$\frac{1AU}{1pc} = \frac{ x_T}{3.62 pc} $$ $$ \rightarrow x_T = 3.62 AU$$

Edit: further explanation

This is a distance of 1AU.

This is an arcsecond, a certain angle (actually looks a lot narrower but that would be hard to draw)

If you put them together to a right triangle, the length of the side adjacent to $\mu$ will always be 30856780000000km. For convenience, we call this distance one parsec. Like how we call 5280 feet a mile.

You can measure distances in parsecs anywhere in space.

Knowing that whereever you have a triangle with an angle of one arcsecond, the ratio between opposite side and hypotenuse is 1AU:1pc can be applied to many situations. Anywhere you can draw a triangle with an angle of 1 arcsecond and you already know one of the side lengths, you now almost automatically know the other one too.

It doesn't matter what three stars or points in space are at the vertices of the triangle. If you can draw a triangle with an angle 1arcsecond, you can use this rule to know the missing length. That's why some diagrams look different.

One such situation is when you are looking out from earth, know that the angle the star appeared to traverse in the sky is 1 arcsecond, and know the distance to the star.