2

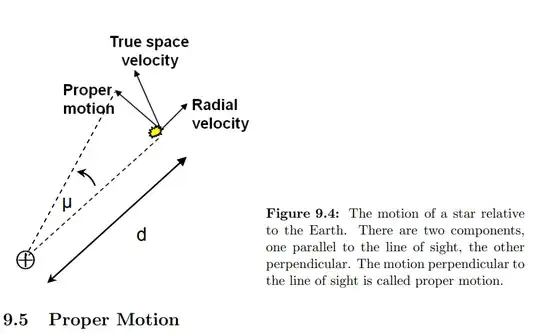
Proper motion

If $\mu$ is the proper motion of a star in arcseconds per year, and $d$ is the star’s distance from us, then the transverse speed, $v_t$ will be $$v_t=d\sin\mu$$ For small motions (assumed for this question) $\sin\mu\approx \mu$

Barnard’s star has a measured parallax of $0.55\, \rm{arcsec}$. Barnard’s star also has a proper motion of $10.3$ arcsec per year. What component of the star’s velocity relative to the Sun can be deduced from the proper motion? Calculate this component, in $\rm{kms^{−1}}$.

This is the way I thought the transverse speed should be calculated:

Firstly, $d$, can be determined through the trigonometric parallax, $p$: $$d(\rm{pc})=\frac{1}{p(\rm{arcsec})}$$

For a parallax of $0.55\, \rm{arcsec}$

$$d=\frac{1}{0.55}\approx 1.8 {\rm\, pc}$$ Using the fact that $1\,\rm{pc}=3.1\times 10^{16}\,\rm{m}$ & $1\, \rm{yr}=3\times 10^7\,\rm{s}$ $$\begin{align}v_t&=d\mu \\&=1.8 \,\rm{pc}\times \frac{3.1\times 10^{16}\rm{m}}{pc}\times\frac{10.3 \,\color{green}{\rm{arcsec}}}{3\times 10^7\,\rm{s}}\\&=\frac{1.8\times 3.1\times 10^{16}\times 10.3\,\rm{m}}{3\times 10^7\,\rm{s}}\\&\approx 1.92\times 10^{10}\,\rm{m\,s^{-1}}\\&=1920\times 10^7 \,\rm{km\,s^{-1}} \end{align}$$

The part marked green I have omitted since it is dimensionless.

Before asking this I searched for an answer and found this similar question which also omitted a dimensionless unit (which was radians in their case).

The correct answer is

At the distance of Barnard’s star ($1.8 \,\rm{pc}$), $\bbox[yellow]{{\text{an angle of} \, 10.3 \, \rm{arcsec}\, \text{corresponds to}\, 1.8 \times 10.3 \, \rm{AU}}}$, or $1.8 \times 10.3 \times 1.5 × 10^{11}\,\rm{m}$. This is the distance covered in $1$ year, or $\sim 3 \times 10^7\,\rm{s}$, yielding a velocity of about $90 \, \rm{km\, s^{−1}}$.

I have highlighted in yellow the part I do not understand in the solution. Why does $\bbox[yellow,5px,border:2px solid red]{{\text{an angle of} \, 10.3 \, \rm{arcsec}\, \text{correspond to}\, 1.8 \times 10.3 \, \rm{AU}}}\,$?

Specifically, I don't understand why the $\rm {AU}$ comes into this (I thought the distances were in $\rm{pc}$, not $\rm{AU}$).

BLAZE
  • 2,441
  • 3
  • 35
  • 64

3 Answers3

3

Your first problem is just that you haven't converted 10.3 arcseconds into radians, which you need to do before attempting any trigonometry.

Your second problem is more subtle. The definition of Parallax is that the 1 au radius of the Earth's orbit around the Sun causes an angular change of 1 arcsecond in the apparent position of a star that is 1 parsec distant. But this definition can be extended to any angular displacement. Thus if a star is 1 pc away, a proper motion displacement of $x$ arcseconds/year means it is moving at $x$ au/year. If it is at a different distance we just scale up by the distance in parsecs.

Why do parsecs come into it? Because the definition of a parsec is based on the astronomical unit! Welcome to the bottom rungs of the distance ladder.

BLAZE
  • 2,441
  • 3
  • 35
  • 64
ProfRob
  • 141,325
2

The small angle approximation $\sin \theta = \theta$ is only good for angles measured in radians.

You need to convert your 10.3 arc seconds to a much smaller number of radians.

BLAZE
  • 2,441
  • 3
  • 35
  • 64
Bob Jacobsen
  • 14,649
0

Why does an angle of $10.3\,\mathrm{arcsec}$ correspond to $1.8 \times 10.3\,\mathrm{AU}$?

Since $1\,\mathrm{arcsec}\lt\lt 1$ then $\tan\theta\approx\theta$ and you can just use the formula that defines the parsec:

$\frac{1\,\mathrm{AU}}{1\,\mathrm{pc}}=1\,\mathrm{arcsec}$

Then you scale up the formula by multiplying both sides by $10.3 \times 1.8\, \mathrm{pc}$:

$10.3 \times 1.8\, \mathrm{pc}\times\frac{1\,\mathrm{AU}}{1\,\mathrm{pc}}=10.3 \times 1.8\, \mathrm{pc}\,\mathrm{arcsec}$

The LHS is $10.3 \times 1.8\, \mathrm{AU}$ as requested, and is approximately $2.8 \times 10^{12}\,\mathrm{m}$ (taking $1\, \mathrm{AU}=1.5\times 10^{11}\,\mathrm{m}$).

Care must be taken when calculating the RHS (as mentioned in other answers), since the arcsec must be converted to radians:

The RHS is $10.3 \times 1.8 \times 3.1 \times 10^{16} \times\frac{1}{3600}\times \frac{\pi}{180}\approx 2.8\times 10^{12}$ as before