Very good question! There are parts of your analysis which are correct: a stationary state for a particle in a box is indeed not a state of definite momentum, and therefore one cannot speak of the momentum of such a state. However, one can speak of the possible values of momentum one could obtain, even if such a measurement were made on a state which isn't a state of definite momentum. This is what the question is asking. You are also correct about the expectation value of the momentum: it will be zero. This is a general result for any real wavefunction. However, even if the possible momenta allowed are $+p_0$ and $-p_0$ with equal probability, the expectation value is clearly zero!
Let's see if I can motivate how the answer you were provided with was obtained. (There is, however, a subtlety here, which I will come back to in a bit.) Also as a side-node, I prefer to use $\hbar = h/2\pi$ instead of $h$, so my answers may look a little different from the answer key, but they are the same.
Essentially, the stationary state solution $\psi(x) = \sin(10\pi x/a)$ can be thought of as the superposition of two waves, one with momentum $10\pi\hbar/a$ and the other with momentum $-10\pi\hbar/a$ (just like standing waves on a string can be thought of as the superposition of two travelling waves, one moving right and the other moving left). Let's try to derive this explicitly by moving to the Momentum Space representation of the wavefunction. You should know that the position and momentum space wavefunctions are related by a Fourier transform: $$\varphi(p) = \frac{1}{\sqrt{2\pi\hbar}}\int_{-\infty}^\infty \text{d}x\,\,\psi(x) e^{-i p x/\hbar},$$ and if you plug in the wavefunction above, you can easily see that the solution is: $$\varphi(p) \propto \delta\left(p - \frac{10\pi \hbar}{a}\right) + \delta \left(p + \frac{10\pi \hbar}{a}\right).$$
In other words, the momentum space wavefunction is a sum of two "Dirac Delta functions": two sharp "spikes" at $\pm p_0 = \pm 10\pi \hbar /a = \pm 5 h /a$. This means that if the momentum of this state were measured, the only values that have a non-zero probability of being detected are $\pm 5h/a$.
You can easily show the above relation by using the definition of the $\delta-$function: $$\delta(p-p_0) = \frac{1}{\sqrt{2\pi \hbar}} \int_{-\infty}^\infty\text{d}x\,\, e^{-i (p-p_0) x/\hbar}.$$
(In fact, you don't even have to work this out explicitly: you could just write out the wavefunction as a sum of two complex exponentials, and this should immediately be clear.)
So, to summarise the above analysis: you don't need to be in a state of definite momentum in order to know which values of momentum will be measured. In the above case, the wavefunction is not a state of definite momentum, however we can say for certainty that the result of a momentum measurement will either be $+p_0$ or $-p_0$, with equal probability.
Right, so that's the justification for the "solution" that you've been provided. The only problem is that this analysis is wrong (or at least not strictly correct) for a particle in a box! In the above analysis, we have assumed (as most people do) that $\psi(x) = \sqrt{2/a} \sin(n \pi x/a)$. However, this is incomplete. The actual wavefunction is: $$\psi(x) = \begin{cases}\sqrt{\frac{2}{a}} \sin(n \pi x/a) \quad \quad &0<x<a,\\ 0 & \text{otherwise.} \end{cases}$$
Plugging this function into the Fourier Transform formula, we get something a little more complicated (note the different limits):
\begin{aligned}\varphi(p) = \sqrt{\frac{2}{a}}\int_{0}^a \sin(n \pi x/a) e^{ipx/\hbar} &= \sqrt{\frac{2}{a}}\frac{\pi a n \hbar^2 \left((-1)^{n}e^{-i a p/\hbar}-1\right)}{a^2 p^2 - \pi ^2 n^2 \hbar^2}\\~\\ &= \sqrt{\frac{2}{a}}\frac{p_0 \hbar}{p^2 - p_0^2} \left((-1)^n e^{-iap/\hbar}-1 \right), \end{aligned}
where I've defined $p_0 = n\pi \hbar/a$. This no longer represents two infinitely sharp spikes in momentum space. If I set $n=10$ (as in your question), and choose $a=1=\hbar$, the probability distribution $|\varphi(p)|^2$ looks like: 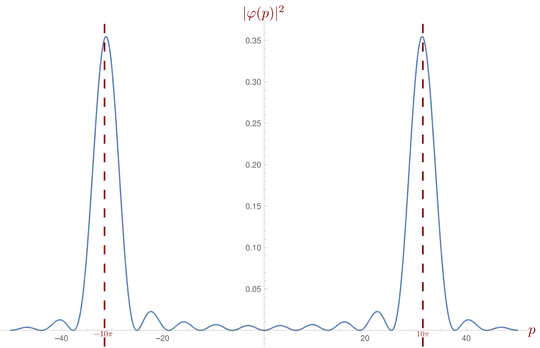
As you can see, there are indeed two spikes, each centred at $\pm p_0 = \pm 10 \pi$ respectively, however unlike our earlier analysis, these spikes have some width, and there is also a small (but non-zero) probability that the particle may be measured having other momenta, as can be seen by the little "bumps" in the probability distribution.
So why does the first analysis work? Well, that analysis assumes the wavefunction to be a sine over all space, and therefore can be written as the superposition of two complex exponentials (i.e., two "plane waves") with equal and opposite momenta. This could be an acceptable wavefunction for a free particle, for example. However, the minute we confine the particle to a box, we require the wavefunction to be zero outside the box, and achieving this requires many more plane waves of different momenta. Of course, the momenta that contribute the most are still the ones you'd naively assume, but there are important contributions from nearby values as well.
