Intro
I think your question is a bit misguided because you are trying to draw a straight axis along which the time would be measured. Instead time measured by any observer, the only time that matters for that observer in most cases, is it's proper time. To measure proper-time you need to measure the arc-length of a curve, that is the world-line of the observer. Once you understand that you will no longer need to draw scores of dashed lines. Space-time diagrams will still remain useful of course.
So the way I will answer your question is to very quickly introduce proper time and how it relates to arc-length. I will then resolve the twin paradox by showing that if the two twins ($A$ and $B$) meet at one event, then split, then meet again, the twin that did not accelerate will measure greatest time lapse (will be older).
World-line
Position of any point-like object in 4d spacetime can be given by $x^\mu=\left(ct, \mathbf{r}\right)^\mu=\left(ct,x,y,z\right)$. Here I will always use Cartesian coordinates. This is the position assigned to an object by some inertial (lab-frame) observer.
We tend to want to discuss objects that do not suddenly disappear, so instead of a single position, all objects will have a world-line, a continuous line that gives the position of the object at all times. You drew some world-lines in your sketches.
Because world-line is indeed a line, it can be parametrized by a single (real) number. One possible way to parametrize world-line is by lab-time, i.e.
$$
x^\mu\left(t\right)=\left(ct,\,\mathbf{r}\left(t\right)\right)^\mu
$$
This is easy, and often necessary to tie mathematics to observable phenomena, but such description is theoretically inconvenient since your time might be different to mine if we are moving relative to each other.
A different approach is to tie the parametrisation to arc-length of the curve. Imagine there are two events:
$$
\begin{align}
x^\mu_1&=\left(ct,\mathbf{r}\right)^\mu \\
x^\mu_2&=\left(ct+c\delta t,\mathbf{r}+\delta\mathbf{r}\right)^\mu
\end{align}
$$
that are close to each other. I would be glad to be corrected here, but as far as I understand, definition of 'close' here would rely on $\mathbb{R}^4$ topology of spacetime.
Next, we can compute the following quantity:
$$
ds = \sqrt{c^2 \left(\delta t\right)^2 - \left(\delta\mathbf{r}.\delta\mathbf{r}\right)}
$$
which would be the invariant 'distance' between $x^\mu_1$ and $x^\mu_2$. Invariant because all inertial observers would agree on this distance. Here, for simplicity we shall constrain ourselves to world-lines of objects moving at sub-liminal speeds. Which would mean that for all closely-spaced events on the world-line of the object $ds>0$.
We can then define some point on the world-line, $x_0^\mu$ to be at $s=0$, and find the invariant distance from that point to any other point, $x^\mu_1$, on the world-line, by integrating:
$$
s_1 = \int_{x_0}^{x_1} ds = \int_{x_0}^{x_1} \sqrt{c^2 \left(d t\right)^2 - \left(\delta\mathbf{r}.\delta\mathbf{r}\right)}
$$
Don't worry about actually doing the integral, it is enough to understand it is possible to do it. The beuaty of this approach is that any two observers will agree that 'distance' from $x_0^\mu$ to $x_1^\mu$ along the curve, as outlined above, which I will call arc-length is $s_1$.
So now we can simply parametrize all points on the curve by this arc-length.
$$
x^\mu\left(s\right)=\left(ct\left(s\right),\,\mathbf{r}\left(s\right)\right)^\mu
$$
Proper time
Now imagine an observer sitting in some rocket or something like that and holding on to clock. Irrespective of whether the observer (and the clock) is inertial or accelerating, one can always imagine an inertial frame in which observer is instantaneously at rest (and next second observer may no longer be at rest in this frame). Lets call it the instantaneous rest frame (I recall it being called the tangential rest frame as well). In that instantaneous rest-frame, $\bar{S}$ the world-line of the clock will be
$$
\bar{x}^\mu\left(s\right)=\left(c\bar{t}\left(s\right),\mathbf{0}\right)^\mu
$$
Of course this is only valid for the time at which the clock remains nearly at rest in $\bar{S}$. Consider the arc-length between two closely spaced events $\bar{x}^\mu\left(s\right)$ and $\bar{x}^\mu\left(s+\delta s\right)=\bar{x}^\mu\left(s\right)+\left(c\delta\bar{t},\mathbf{0}\right)^\mu$. Here $\delta \bar{t}$ is the time-difference that would be measured by observer's clock (same as time in $\bar{S}$ since clock is instantaneously at rest in $\bar{S}$). By definition of the arc-length, it is:
$$
\delta s=\sqrt{c^2\left(\delta\bar{t}\right)^2}=c\delta\bar{t}
$$
Since speed of light, $c$, is constant one can see that observer's clock is measuring the arc-length in 'light-years' (i.e. multiply the observer's time by speed of light to get the arc-length). Based on this insight we define the proper time $\tau=s/c$. This is the time measured by observer that is moving along some world-line, but it is also the arc-length of that world-line measured in units of time. We can therefore parametrize any world-line by it's proper time:
$$
x^\mu\left(\tau\right)=\left(ct\left(\tau\right),\,\mathbf{r}\left(\tau\right)\right)^\mu
$$
Curved world-lines & twin paradox
Lets imagine two events $x_1^\mu$ and $x_2^\mu$ and assume that it is possible to get from $x_1^\mu$ to $x_2^\mu$ at sub-luminal speed. Lets imagine two paths between these two points. One path is that of an object $A$ that is not accelerating, another of object $B$ that is accelerating, and then decelerating (or it would not meet with $A$). The first world line will be straight, the second one will be curved (I will not explain line curvature here any further since it can be avoided).
Assume that clocks of $A$ and $B$ are synchronized at $x_1^\mu$ ($\tau_A=\tau_B=0$ at $x_1^\mu$).
One can show that proper time measured by $A$ at point $x_2^\mu$, i.e. $\tau_{A@2}$ will be the longest possible for all world-lines that go through both $x_1^\mu$ and $x_2^\mu$ and are time-like at all points (i.e. only sub-luminal speeds of travel)
How? Consider the world-line of observer $A$ in its own rest-frame ($S'$):
$$
{x'}_A^\mu \left(t'\right) ={x'_1}^\mu + \left(ct',\mathbf{0}\right)^\mu
$$
Where $t'=\tau_A$ ($A$'s rest frame). Therefore ${x'_2}^\mu=\left(c\tau_{A@2},\mathbf{0}\right)^\mu$. What is the world-line of $B$ in $S'$? Lets say that velocity of $B$, as seen by $A$ is $\mathbf{v}_B=\mathbf{v}\left(t'\right)=d\mathbf{r}_B/dt'$, and its position is $\mathbf{r}_B$, therefore $B$-s world-line is:
$$
{x'}_B^\mu \left(t'\right) ={x'_1}^\mu + \left(ct',\mathbf{r}_B\left(t'\right)\right)^\mu,\quad \mathbf{r}_B\left(0\right)=\mathbf{r}_B\left(\tau_{A@2}\right)=\mathbf{0}
$$
What is the arc-length of $B$?
$$
c\tau_{B@2}=\int_{0}^{\tau_{A@2}} \sqrt{c^2 \left(dt'\right)^2-\left(d\mathbf{r}_B\right)^2}=\int_{0}^{\tau_{A@2}} dt'\,\sqrt{c^2 -\left(\mathbf{v}_B\right)^2}
$$
Now you should see that any non-zero speed $\mathbf{v}_B$ along the path of $B$ will lead to reduction in $\tau_{B@2}$, therefore unless $B$ is at rest relative to $A$, the time $\tau_{B@2}$ will be less than that of $\tau_{A@2}$ when they meet again.
That's the twin paradox resolved. $x_1$ is when the two twins meet for the first time, $x_2$ is when they meet again and compare clocks.
Addendum
There seems to be a lot of questions on 'accelerated reference frames'. I will try to address it, but happy to be corrected. A proper reference on this is chapter 6 'Accelerated Observers' from Misner, Thorne, Wheeler Gravitation (first part of the book is on Special Relativity).
So what do we mean by reference frame? It would seem that Wiki's definition is appropriate:
A frame at a point x ∈ X is an ordered basis for the vector space Ex
the key here is this basis of vectors. Lets say you have an object that is moving at some, possibly non-constant, speed relative to lab frame. The world line is $x^\mu=x^\mu\left(\tau\right)$, where $\tau$ is the proper time. Consider some point $x^\mu_1=x^\mu\left(\tau_1\right)$. At that point you can always identify the tangent to the world-line, $u_1^\mu=\left(dx^\mu/d\tau\right)_{@\tau_1}$. This is known as four-velocity, but the name is not important. Once you have the four-velocity, you can find three more vectors that are perpendicular to it, and this tetrad of basis vectors, call them $\hat{\tau}^\mu=u^\mu/c,\,\hat{x}^\mu,\,\hat{y}^\mu,\,\hat{z}^\mu$ will allow you to express any vector at that point $x^\mu_1$. What you could try to do next is draw four sets of straight lines, parallel to your basis vectors, to get something like the white grid on the picture below, but in 4d.
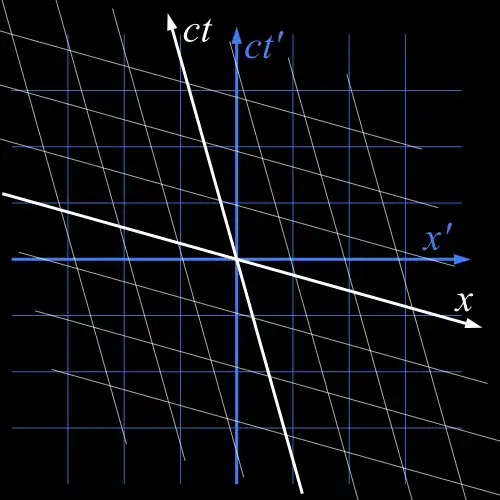
This is nice, but you must remember that you generated this grid from a single tangent at a specific point. Will you get the same grid if you use a tangent to the world-line at some other point? For inertial observers you will - their world-lines are straight. For accelerated observers you will not - their world-lines are curved. Coming back to the definition of frame, for accelerated observers different points on the world-line have different frames, i.e. different basis vectors.
You can pretend that the curved line is actually straight, but only if you limit your interest to the region where the curvature of the world-line is too small to notice. In this sense you can talk about the rest-frame for an accelerating observer, but it is local.
Another approach is to have a global reference frame, but your accelerating observer will only be at rest in that frame for a short period of time. This would be the instantaneous rest-frame. I prefer the second approach.