0

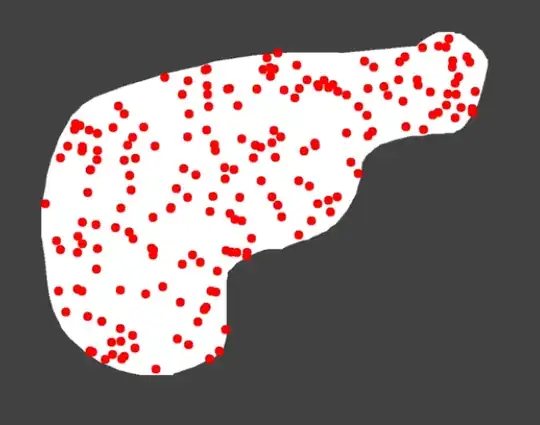
I was working on a program that generates random tiles in a given shape. To do this I generated random points inside the shape and would use them to color the tiles.

Random

However, after noticing clumping of the points, I decided to create a way to spread them out more. My first thought was to simulate the points repelling each other, basically using the same equation as Coulomb's Law (but simplified and with acceleration instead):

Coulomb's Law

$$\boldsymbol{\vec{F}}=K\frac{Q_1 * Q_2}{R^2} \boldsymbol{\hat{r}}$$

Simplified for my use:

$$\boldsymbol{\vec{A}}=-\frac{K}{R^2}\boldsymbol{\hat{r}}$$

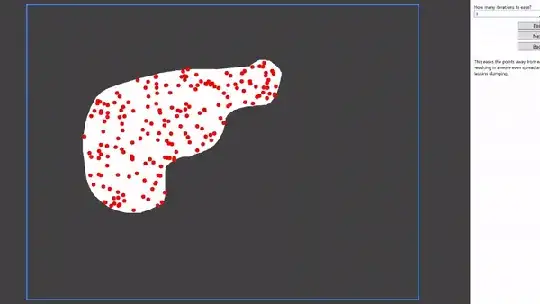
I them clamped the positions of the points so that they lie within a set shape. Running this "simulation", here's what I got:

The simulation

Unfortunately, rather than spreading out more evenly, they all accumulated on the edges of the shape. While this was annoying, I vaguely remembered something in Physics class about how electrons accumulate on the surface of a wire. So my question is: If electrons were placed randomly in a closed shape, would they accumulate on the surface of the shape as shown in my program? Or did I just screw up my code :P

nreh
  • 268
  • 1
  • 11

1 Answers1

1

If electrons were placed randomly in a closed shape, would they accumulate on the surface of the shape as shown in my program?

Yes, if that shape is enclosing the surface of a conductor. However, since you did not simulate a conducting material, I think this is a coincidence. Your simulation, by looking at the initial configuration in the second gif, begins with some random distribution of points within a defined boundary, and then those points move under the acceleration that you specified which causes them to move away from each other and so they have nowhere else to go but outward and get blocked by the surface of the shape. This, I think, is further shown by the few points that remain away from the edge of the shape, since they have managed to find a (seemingly) stable position.

Daddy Kropotkin
  • 2,790