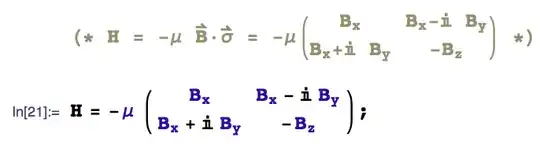Heisenberg equation of motion — why is $\vec{\sigma}_H=\vec{\sigma}$?

Question

Trying to obtaining the Heisenberg EOM ( "for $\vec{\sigma}$" ) for the following Hamiltonian

$$ H = - \mu \vec{B}\cdot\vec{\sigma} $$ where the magnetic field $\vec{B}$ is generic for now, $\vec{B}=\{B_x,B_y,B_z\}$, and $\vec{\sigma}$ is the Pauli vector (of Pauli matrices).

The Heisenberg EOM reads

$$ \frac{d}{dt} A(t)_H = \frac{i}{\hbar} [H,A(t)_H] + (\frac{\partial A_H}{\partial t})_H $$

The (well my professor's, and so I would like to mimic her style as she's brilliant) solutions to the problem we got after trying this for HW last week makes a step that I am confused about:

Why is the operator $\vec{\sigma}$ not transformed to the Heisenberg picture? Ought we to first send

$$ \vec{\sigma} \rightarrow \vec{\sigma}_H=e^{\frac{it}{\hbar}H}\vec{\sigma}e^{\frac{-it}{\hbar}H} $$

My only thought is that my professor already did so! See the following work from a similar problem I found on the web. The Hamiltonian in this work's case is more specific,

$$ H=-B \sigma_x $$

In this case, using Mathematica enables us to show that for the case of $\sigma_x$,

$$ (\sigma_x)_H = e^{\frac{it}{\hbar}H} \sigma_x e^{\frac{-it}{\hbar}H} = \sigma_x $$

The following code verifies it:

MatrixForm[Simplify[MatrixExp[i t/h PauliMatrix[1]].PauliMatrix[1].MatrixExp[-i t/h PauliMatrix[1] ]]]

Now... if I define my generic Hamiltonian:

where I use the Pauli vector now for the more generic Hamiltonian instead of one of the matrices like the example above... the same formula for $(\sigma_x)_H$ is .... disturbing.

Can someone point out my mistake (computational or conceptual) and point me to how I can show $\vec{\sigma}_H=\vec{\sigma}$

Edit: [Incorrect!]

I was thinking about the following but it is still a complete (or/nor coded correctly) idea

Edit based on @ZeroTheHero's Baker–Campbell–Hausdorff formula insight

using this form of the BCH formula (eq 3 here)

$$ e^A B e^{-A} = B + [A,B] + 1/2[A,[A,B]] + ... $$

shouldn't I be able to say

$\begin{eqnarray*} (\vec{\sigma})_H &=& e^{\frac{it}{\hbar}H} \vec{\sigma} e^{\frac{-it}{\hbar}H} \\ &=& \vec{\sigma} + [H,\vec{\sigma}] + ... \\ &=& \vec{\sigma} -\mu [\vec{B} \cdot \vec{\sigma},\vec{\sigma}] ... \\ &=& \vec{\sigma}- \mu \vec{B} [\vec{\sigma},\vec{\sigma}] + ... \\ &=& \vec{\sigma}+ 0 \\ &=& \vec{\sigma} \end{eqnarray*}$

This seems correct to me, but if so, the result $[H,\vec{\sigma}]=0$ reduced the Heisenberg EOM to

$$ \frac{d}{dt} \vec{\sigma} = 0 $$

which I know to be false... :/

My thoughts at the moment is that my $[H,\vec{\sigma}]$ is wrong based on my professor's calculation above where she does NOT factor out the constant $\vec{B}$. I was motivated to factor out based on this Stack answer.

Answer 1

Clearly $\exp(\hat A)\hat A\exp(-\hat A)=\hat A$ by Baker-Campbell-Hausdorff. Here, set $\hat A=\hat H=-it\mu\vec B\cdot \vec \sigma/\hbar$.

Note that \begin{align} \exp(-i t\mu \vec B\cdot \vec \sigma/\hbar)\ne \exp(-it B_x\sigma_x)\exp(-it B_y\sigma_y)\exp(-it B_z\sigma_z) \end{align} or any other kind of factorization suggested by your snippet of Mma code since in general $\exp(A+B)\ne \exp(A)\exp(B)$. The correct implementation would be to compute $-it\mu\vec B\cdot\vec \sigma/\hbar$ as a single matrix and then exponential this single matrix.